Следующая замечательная конструкция была предложена Пьером де Ферма в 1638 году и переоткрыта Клиффордом и Штуди в XIX веке. Текст Ферма не дает никаких возможностей для истолкования его в инфинитезимальном смысле, в духе Лейбница, или в смысле теории пределов. Напротив, это чисто алгебраический текст, притом абсолютно строгий.
1. Кольцо дуальных чисел. Пусть

- произвольное поле, например,

a

- не принадлежащий

элемент такой, что

Рассмотрим множество
![$K[d],$ $K[d],$](https://dxdy-04.korotkov.co.uk/f/b/4/b/b4bafbb5a62fc8d1a7021dea07b3ba3c82.png)
элементами которого являются формальные линейные комбинации

и

с коэффициентами из

(мы пишем просто

вместо

причем

в том и только том случае, когда

и

), сложение покомпонентное, а умножение продолжает умножение

и

по линейности, иными словами, для

имеем

Построенное так кольцо называется
кольцом дуальных чисел над
 2. Нильпотенты.
2. Нильпотенты. В частности, в
![$K[d]$ $K[d]$](https://dxdy-04.korotkov.co.uk/f/f/3/4/f34df0fcbc2fe4305a2220e6407a34de82.png)
имеем

для любого

Элементы
![$dy\in K[d]$ $dy\in K[d]$](https://dxdy-04.korotkov.co.uk/f/3/9/f/39f4c5754528a3ca4fb54b605e28518982.png)
являются
актуально бесконечно малыми первого порядка, рассматриваемыми с точностью до бесконечно малых второго порядка (понятия, относящиеся к актуально бесконечно малым, называются обычно
инфинитезимальными - 'infinitesimal'). Это значит, что кольцо
![$K[d]$ $K[d]$](https://dxdy-04.korotkov.co.uk/f/f/3/4/f34df0fcbc2fe4305a2220e6407a34de82.png)
уже достаточно для определения
первых производных, причем в нем производная находится непосредственно как
отношение бесконечно малых, а не как продел отношений конечных величин.
3. Производные. Функция

называется
дифференцируемой, если ее можно продолжить на
![$K[d]$ $K[d]$](https://dxdy-04.korotkov.co.uk/f/f/3/4/f34df0fcbc2fe4305a2220e6407a34de82.png)
так, чтобы отношение

называемое
производной 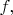
не зависело от выбора

Для этого необходимо (но, вообще говоря, не достаточно), чтобы

было бесконечно малой. Разумеется, для дифференцируемой функции мы можем определить производную так, как это делается в анализе, заменив

на

:

замечательно, что нам не приходится при этом писать знака предела!
4. Производные многочленов. ...
5. Производные экспоненты и логарифма. ...
6. Производные тригонометрических функций. ...
Комментарий 2. Эта идея легко переносится и на производные высших порядков. при этом вместо кольца двойных чисел нужно рассматривать его обобщение - кольцо
усеченных многочленов ![$K[t]/(t^n)$ $K[t]/(t^n)$](https://dxdy-01.korotkov.co.uk/f/8/3/0/830b5451f2a71c2557e085ddd226cd3e82.png)
которое мы введем в § ?. Разумеется, единственная сложность здесь доопределить функцию, априори заданную на

на всем
![$K[t]/(t^n).$ $K[t]/(t^n).$](https://dxdy-02.korotkov.co.uk/f/1/6/a/16a6ba520301f1780cc560ce77ed6dcc82.png)
Конечно, для функций, заданных рядами (а
только такие функции и рассматривались классиками!) этого вопроса не возникает.
Комментарий 3. Построить чисто алгебраическую версию дифференциального исчисления
бесконечного порядка
не в пример сложнее. Наиболее известный подход предложен А.Робинсоном в его 'нестандартном анализе'...