Найти рациональные решения уравнения

[Коровьев]

Найти рациональные решения уравнения

$\[ x^2 + y^2 + z^4 = 1 \] $

p.s. Есть двухпараметрическое решение

[Shadow]

Решить вряд ли смогу, но найти решения (серию) можно. Решениями уравнения $a^2+b^2+c^2=1$ являются:

$a=\dfrac{2m}{m^2+n^2+1},\;b=\dfrac{2n}{m^2+n^2+1},\;c=\dfrac{n^2-m^2+1}{m^2+n^2+1}$

Выберем, напр. первое:

$z^2=\dfrac{2m}{m^2+n^2+1}$ положим $m=2u^2,n=2u^4$, получим $z=\dfrac{2u}{2u^4+1}$

Но оно однопараметрическое

[Shadow]

Двухпараметрическое станет, после $m=2u^2$ - числитель квадрат, знаменатель:

$4u^4+n^2+1=d^2$

$(d-n)(d+n)=4u^4+1$

$\\d-n=v\\ d+n=\dfrac{4u^4+1}{v}\\ \\ n=\dfrac{4u^4+1-v^2}{2v}$

Вот уже двухпараметрическое...но все равно неполное. Арифметику не проверял...

[Коровьев]

Это тождество в решении используется, но по другому

Рассмотрите
$\[ x^2 + y^2 = \left( {1 + z^2 } \right)\left( {1 - z^2 } \right) \]$

[Shadow]

Если правильно улавливаю мысль, $x^2+y^2$ разлагается на множители, кажды из которых представим в виде $a^2+b^2$, тоесть, $1-z^2=a^2+b^2$

и воспользоватся тождеством $(a^2+b^2)(z^2+1)=(az+b)^2+(a-bz)^2$

$a^2+b^2+z^2=1$ имеет двухпараметрическое решение, значит $x=az+b,\;y=a-bz$

Пока не знаю все ли тут корректно, будет ли решение полным.

-- 29.10.2015, 20:20 --

Shadow в сообщении #1068183 писал(а):

Пока не знаю все ли тут корректно, будет ли решение полным.

Кажется все ок. Ведь для любой рацоналной тройки $(x,y,z)$ существует рациональная пара $(a,b)$ такая, что

$\\x=az+b\\ y=a-bz$

и воспользоватся тождеством.

Получается такая жесть, много не проверял:

$x=\dfrac{2(m^3+m^2n-mn^2+m+n^3+n)}{(m^2+n^2+1)^2}$

$y=\dfrac{2(m^3-m^2n+mn^2+m+n^3-n)}{(m^2+n^2+1)^2}$

$z=\dfrac{m^2-n^2+1}{m^2+n^2+1}$

[Коровьев]

Всё правильно.
Можно доказать, что если для рациональных чисел выполняется

$c(a^2+b^2)=m^2+n^2$

то $c$ является квадратом или представимо суммой квадратов рациональных чисел.
Следовательно, в задаче
$1-z^2=k^2+t^2$

Приведённое ранее тождество описывает все возможные тройки рациональных чисел (это тоже доказывается).
За $z$ можно взять любое из трёх приведённых выражений для $a,b,c $
Так как
$\[ x^2 + y^2 = \left( {k^2 + t^2 } \right)\left( {1 + z^2 } \right) = \left( {k - tz} \right)^2 + \left( {t + kz} \right)^2 = \left( {k + tz} \right)^2 + \left( {t - kz} \right)^2 \]$

то получим 6 вариантов двухпараметрических решений и по логике доказательства это все решения в обезличенных переменных.
В конкретных числах возможны и другие представления произведения в виде суммы двух квадратов. Тут что-то сказать сложно.

Результат этой задачи позволяет найти рациональные решения уравнения

$x^2+y^4+z^4=1$

Поищем!

А там недалеко и до уравнения
$x^4+y^4+z^4=1$

[Shadow]

Shadow в сообщении #1068114 писал(а):

Решениями уравнения $a^2+b^2+c^2=1$ являются:

$a=\dfrac{2m}{m^2+n^2+1},\;b=\dfrac{2n}{m^2+n^2+1},\;c=\dfrac{n^2-m^2+1}{m^2+n^2+1}$

Ошибочка,

$c=\dfrac{m^2+n^2-1}{m^2+n^2+1}$

и другие надо исправить

[Коровьев]

Я "немного" преувеличил число вариантов решения. Реально всего один вариант.

Для снижения громоздкости обозначим

$$\[ S_{a,b} = \frac{{2a}}{{1 + a^2 + b^2 }} \] $

$$\[ S_{b,a} = \frac{{2b}}{{1 + a^2 + b^2 }} \] $

$$\[ C_{a,b} = C_{b,a} = \frac{{1 - a^2 - b^2 }}{{1 + a^2 + b^2 }} \] $

Тогда

$\[ \left( {S_{a,b} } \right)^2 + \left( {S_{b,a} } \right)^2 + \left( {C_{a,b} } \right)^2 = 1 \]$

Теперь к задаче.

Варианты
$\[ \left\{ \begin{array}{l} z = S_{a,b} \\ z = S_{b,a} \\ \end{array} \right. \] $
отличаются только перестановкой переменных и можно считать, что это один вариант.


$$\[ x^2 + y^2 = \left( {k^2 + t^2 } \right)\left( {1 + z^2 } \right) = \left( {k - tz} \right)^2 + \left( {t + kz} \right)^2 = \left( {k + tz} \right)^2 + \left( {t - kz} \right)^2 \]$
Здесь тоже один вариант, если иметь ввиду, что $t$ может быть и отрицательным.

И самое интересное.
Функции $S_{x,y}$ и $C_{x,y}$ рационально эквивалентны. То есть, существует рациональное преобразование одной функции в другую и обратно.

$$\[ S_{a,b} = C_{x,y} \Rightarrow x = \frac{{C_{a,b} }}{{S_{a,b} + 1}},y = \frac{{S_{b,a} }}{{S_{a,b} + 1}} \]$

$$\[ C_{x,y} = S_{a,b} \Rightarrow a = \frac{{1 + S_{y,x} }}{{C_{x,y} }},b = \frac{{S_{x,y} }}{{C_{x,y} }} \]$

Т.о. практически мы имеем один вариант решения, который охватывает все решения
уравнения.
Выберем вариант Shadowа (с исправлением)

$$\[ x = 2\frac{{\left( {a^3 + a^2 b + ab^2 + b^3 } \right) + \left( {a - b} \right)}}{{\left( {1 + a^2 + b^2 } \right)^2 }} \]$

$$\[ y = 2\frac{{\left( { - a^3 + a^2 b - ab^2 + b^3 } \right) + \left( {a + b} \right)}}{{\left( {1 + a^2 + b^2 } \right)^2 }} \]$

$$\[ z = \frac{{1 - a^2 - b^2 }}{{1 + a^2 + b^2 }} \]$

Все остальные варианты рационально эквивалентны выбранному.

[Shadow]

Коровьев в сообщении #1068430 писал(а):

Т.о. практически мы имеем один вариант решения, который охватывает все решения

кроме $x=0,y=0,z=-1$ - единственное исключение.

[scwec]

Замечу, что параметрическое решение уравнения $a^2+b^2+c^2=1$
$a=\dfrac{2m}{m^2+n^2+1},b=\dfrac{2n}{m^2+n^2+1},c=\dfrac{m^2+n^2-1}{m^2+n^2+1}$
не является полным. Пример - три дроби $3/37,8/37,36/37$ в качестве $a,b,c$ в любом порядке.
Может быть, лучше было воспользоваться полным решением этого уравнения
$a=\dfrac{m^2+n^2-p^2-q^2}{m^2+n^2+p^2+q^2}$
$b=2\dfrac{mp+nq}{m^2+n^2+p^2+q^2}$
$c=2\dfrac{np-mq}{m^2+n^2+p^2+q^2}$
Само по себе изложенное решение нравится.

[Коровьев]

Надо же!
А я всё время считал что эта формула полная, тем более, что выводится она в две строчки.
В этой теме я получил эту расширенную формулу для рац.точек на единичном шаре.
Но там нет доказательства её полноты (хотя я там и написал, что это все рац.точки )
Интересно, полная она или нет. Слегка порылся, но ничего об этом не нашёл.
Для единичного круга у Острика есть доказательство. Мне думается, что метод секущей подойдёт и для единичного шара.

[NSKuber]

scwec
Разве ваш пример не получается выбором $m=3$, $n=8$?

[scwec]

Да, Вы правы. А дроби эти получились из того, что решение уравнения $x^2+y^2+z^2=t^2$
$x=k^2-m^2+n^2,y=2km,z=2mn,t=k^2+m^2+n^2$ в натуральных числах не является полным.
И пример именно $3,36,8,37$. Тоньшей надо работать.

[Коровьев]

По моему, в нижеследующем выводе есть доказательство полноты.

Для любых заданных рациональных $a,b$ найдём такие рациональные $x,y$, чтобы выполнялось

$a^2+b^2=x^2-y^2$

Пусть это уравнение выполняется. Тогда для некого рационального $t$ имеем

$x+y=t$

тогда

$$\[ x - y = \frac{{a^2 + b^2 }}{t} \]$

отсюда

$$\[ x = \frac{{t^2 + a^2 + b^2 }}{{2t}},y = \frac{{t^2 - a^2 - b^2 }}{{2t}} \]$

И это все возможные пары рациональных $x,y$, для которых выполняется исходное уравнение при различных рациональных $t$.
Действительно, для любой пары $x_0,y_0$, если выполняется уравнение, найдётся $t_0$, что выполняется

$x_0-y_0=t_0$

а, значит, выполняются выражения для $x,y$

Окончательно формула имеет вид

$$\[ \left( {\frac{{2ta}}{{t^2 + a^2 + b^2 }}} \right)^2 + \left( {\frac{{2tb}}{{t^2 + a^2 + b^2 }}} \right)^2 + \left( {\frac{{t^2 - a^2 - b^2 }}{{t^2 + a^2 + b^2 }}} \right)^2 = 1 \]$

верная для любых $t$ и в частности, для $t=1$.

[Shadow]

Решениями в рац. числах уравнения $x^2+y^2+z^2=1$ являются $x=0,y=0,z=+1$, а также

$x=\dfrac{2a}{a^2+b^2+1},\;\; y=\dfrac{2b}{a^2+b^2+1},\;\;\ z=\dfrac{a^2+b^2-1}{a^2+b^2+1},\;\;\forall a,b \in \mathbb{Q} \qquad (1)$

Решение $z=1$ очевидно нельзя получить, гляда на формулу для $z$ и оно единственное такое. Решения получаются (по методу секущих) с помощью подстановки

$x=a(1-z),\;y=b(1-z)\qquad (2)$

что сразу дает ответ на вопрос: при каких значениях параметров получается конкретно некоторое решение $(x,y,z\ne 1)$ - при $a=\dfrac{x}{1-z},\;b=\dfrac{y}{1-z}\qquad (3)$

Полнота: если формул (3) подставить в (1), получим

$\dfrac{2x(1-z)}{x^2+y^2+(1-z)^2},\;\;\dfrac{2y(1-z)}{x^2+y^2+(1-z)^2},\;\;\dfrac{2(x^2+y^2)}{x^2+y^2+(1-z)^2}-1$

и если действительно $x^2+y^2=1-z^2$, получим $x,y,z$

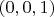
Очевидна и единственость - невозможность при различных значений параметров получить одно и тоже решение. (Геометрически, система (2) задает множество прямых в пространстве проходящих через точку $(0,0,1)$, за исключением "те" в плоскости $y=1$. Различные значения параметров задают различные прямые, но через 2 точки проходит только одна прямая)

И эта параметризация хорошая, потому что пропускает только одно решение. Если, например, зададим

$\\y=ax\\ z=bx+1$

и решаем уравнение относительно $x$, получим другую параметризацию:

$x=\dfrac{2a}{1+a^2+b^2},\;\; y=\dfrac{2ab}{1+a^2+b^2},\;\;\ z=\dfrac{1+a^2-b^2}{1+a^2+b^2}$

и потеряем все решения в плоскости $x=0$. А их там много.
Тоесть, в любом случае теряем всех решений в некоторой плоскости, содержащей базовую точку. И хорошо, если эта плоскость - касательная. Можно, например, придумать "хорошую" параметризацию для уравнения $x^2+y^2+z^2=3$.

scwec в сообщении #1069072 писал(а):

А дроби эти получились из того, что решение уравнения $x^2+y^2+z^2=t^2$
$x=k^2+m^2-n^2,y=2km,z=2mn,t=k^2+m^2+n^2$ в натуральных числах не является полным.
И пример именно $3,36,8,37$.

В таком виде не получается тождество, получается при $x=k^2-m^2+n^2$.