Олимпиада НГУ - 2015

[bot]

(Оффтоп)

iancaple в сообщении #1060540 писал(а):

не все равны между собой

"Не все равные 1" тоже годится. Выбрал просто "различные" - так короче.

[mihiv]

1 курс
5.

$a_1=\sqrt {4n+1}, a_2=\sqrt {n} +\sqrt {n+1},a_3=\sqrt {4n+3},a_2^2=2n+1+2\sqrt {n(n+1)}$ Отсюда получаем неравенства: $4n+1< a_2^2<4n+3$
Так как квадрат натурального числа может иметь вид только $4k$ или $4k+1$, приходим к выводу, что числа $a_1^2, a_2^2, a_3^2$ заключены между двумя последовательными натуральными квадратами (больший из этих двух квадратов $>4n+3$, а меньший $\leqslant 4n+1)$, поэтому $\lfloor a_1\rfloor= \lfloor a_2\rfloor= \lfloor a_3\rfloor $

[bot]

33 областная открытая олимпиада по математике для студентов 1-4 курсов

2 тур (18 октября 2015г.)

1 курс

1. Существует ли многочлен $p(x)$ с целыми коэффициентами, такой что $ p(8) = 1,\, p(25) = 2015 ?$

2. Найти все целые решения уравнения $|x^2-6x-36| + |x^2 +6x-5| = xy.$

3. Все натуральные числа поделены на жирные и тощие. Известно, что, если число $A$ жирное, то $A+5$ тощее, а если число $A$ тощее, то $A+7$ жирное. Может ли среди $2015$ последовательных натуральных чисел быть ровно $1000$ жирных чисел?

4. Числа $a,b,c$ являются длинами сторон некоторого треугольника. Докажите,что

$$\frac{ a }{ b+c-a }+\frac{ b }{c+a - b }+\frac{ c }{a+ b-c } \geqslant 3$$

5. Действительные числа $a, b, c, d$ удовлетворяют неравенствам $48\leqslant a\leqslant b\leqslant c\leqslant d\leqslant 108.$ Определите все возможные значения выражения $\dfrac ab+\dfrac cd.$

2-4 курсы

ДЛЯ ВУЗОВ МАТЕМАТИЧЕСКОГО ПРОФИЛЯ

1. Пусть $a_n$--- сходящаяся последовательность. Может ли последовательность $n(a_{n+1}-a_n)$ быть а) бесконечно большой; б) положительной бесконечно большой?

2. Пусть вещественная функция $f$ непрерывна на отрезке $[0, 1]$ и на его концах принимает равные значения. Докажите, что для любого $n\in\mathbb{N}$ найдутся точки $a, b\in [0,1]$, такие что $b-a=\dfrac{1}{n}$

3. Исследуйте сходимость ряда $\sum\limits_{n=1}^\infty x^{\sqrt n}$ при $x>0.$

4. Линейную комбинацию векторов $n-$мерного пространства назовём нормальной, если сумма коэффициентов в ней равна 1. Докажите, что среди любых $n+2$ векторов
$n-$мерного пространства найдётся вектор, являющийся нормальной комбинацией остальных.

5. Докажите сходимость интеграла $\ds\int\limits_{0}^{\infty}\frac{\ln(1+ {x}^{2})}{1+ {x}^{2}}\,dx$ и вычислите его.


ДЛЯ ВУЗОВ НЕМАТЕМАТИЧЕСКОГО ПРОФИЛЯ

1. Дана последовательность $a_1,\,a_2,\,a_3,\,...\,,a_{2015}$ целых чисел. Переставив их произвольным образом,
получим последовательность $b_1,\,b_2,\,b_3,\,...\,b_{2015}.$ Докажите, что среди чисел $a_i + b_i$ найдется хотя бы одно чётное.

2. Пусть непрерывная на некотором промежутке $I$ функция $f$ взаимно однозначно отображает некоторое конечное подмножество промежутка $I$ на себя.
Докажите, что уравнение $f(x)=x$ разрешимо в промежутке $I.$

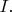
3. Пусть $p(x)$ --- произвольный многочлен с вещественными коэффициентами. Докажите, что многочлен $q(x)=p(x)p'''(x)-p'(x)p''(x)$ имеет хотя бы один вещественный корень.

4. Вычислить предел $\lim\limits_{n\to\infty}\dfrac{1+11+\ldots +\overbrace{11\ldots1}^n}{10^n}.$

5. Пусть функция $f$ определена на $ R,$ непрерывна в точке $0$ и удовлетворяет тождеству $2f(2x) - f(x) = x^2.$ Найдите эту функцию.

[TOTAL]

Цитата:

4. Линейную комбинацию векторов $n-$мерного пространства назовём нормальной, если сумма коэффициентов в ней равна 1. Докажите, что среди любых $n+2$ векторов
$n-$мерного пространства найдётся вектор, являющийся нормальной комбинацией остальных.

Выбрать $n$ векторов так, что два оставшихся через них выражаются: $\displaystyle a=\sum \alpha_i e_i, \;\; b=\sum \beta_i e_i$.
Либо $\sum \alpha_i = 1$, либо найдется подходящий $t$ в $b=\sum \beta_i e_i - t \left( \sum \alpha_i e_i -a \right) $

[kp9r4d]

2-4 курс мат. профиль
1. а) На чётных местах $e^{-n}$ на нечётных $n^{-1/2}$. б) Нет, если бы это было так, то тогда $a_{n+1} - a_{n} = \frac{1}{n} \cdot \alpha(n)$ где $\alpha(n)$ - некоторая последовательность стремящаяся к +бесконечности, просуммировав первые $n-1$ равенств предыдущего вида получим $a_{n}-a_1 = \sum_{k=1}^n \frac{1}{k} \alpha(k)$, откуда $a_{n}$ - не сходится.
2. Было в Зориче :3

-- 19.10.2015, 13:22 --

Во второй пропущено условие $f(b)=f(a)$, скорее всего.

[12d3]

bot в сообщении #1063891 писал(а):

2. Пусть вещественная функция $f$ непрерывна на отрезке $[0, 1]$ и на его концах принимает равные значения. Докажите, что для любого $n\in\mathbb{N}$ найдутся точки $a, b\in [0,1]$, такие что $b-a=\dfrac{1}{n}$

Рассмотрим значения функции в точках $\frac{1}{n},\frac{2}{n},...,\frac{n-1}{n}$. Найдем среди них максимум и минимум. Либо максимум не меньше значения на концах, либо минимум не больше оного. Пусть для определенности это максимум, в точке $\frac{k}{n}$. Рассмотрим $g(x)=f(x+\frac{1}{n})-f(x),x\in [\frac{k-1}{n},\frac{k}{n}]$. Эта новая функция на левом конце маленького отрезочка неотрицательна, а на правом конце неположительна. Значит, в какой-то точке $x_0$ ее значение обращается в ноль. Тогда $a=x_0,\,\,b=x_0+\frac{1}{n}$
UPD Кстати, что будет, если в этой задаче заменить $\frac{1}{n}$ на произвольное $\varepsilon$? Для $\varepsilon > \frac{1}{2}$ легко придумать контрпример. А для остальных?

[RIP]

Тут обсуждалось, в том числе и почему только $1/n$: topic6148.html

[RIP]

bot в сообщении #1063891 писал(а):

5. Докажите сходимость интеграла $\int\limits_{0}^{\infty}\frac{\ln(1+ {x}^{2})}{1+ {x}^{2}}\,dx$ и вычислите его.

Используя науку (гамма-функцию), посчиталось $\displaystyle\int_0^{+\infty}\frac{\ln(1+x^2)}{1+x^2}\,\mathrm{d}x=\pi\ln2$. Нормальное док-во сходу в голову не приходит.

[kp9r4d]

3 Функция монотонно убывает и положительная, поэтому сходимость ряда эквивалентна сходимости интеграла $\int_0^\infty e^{\sqrt{t} \ln(x)} dt$, заменой $\sqrt{t} = p$ нетрудно увидеть, что он сходится (и даже подсчитать точное значение).

-- 19.10.2015, 16:30 --

при условии $0<x<1$ конечно, при условии $x \geqslant 1 $ и так всё понятно.

[RIP]

Попутно посчиталось $\displaystyle\int_0^1\frac{\arcsin x}x\,\mathrm{d}x=\frac{\pi\ln2}2$.

-- Пн 19.10.2015 17:49:53 --

Кажется, если положить $\displaystyle f(a)=\int_0^{+\infty}\frac{\ln(x^2+a^2)}{x^2+1}\,\mathrm{d}x$, то

$$f'(a)=\int_0^{+\infty}\frac{2a\,\mathrm{d}x}{(x^2+1)(x^2+a^2)}=\frac{\pi}{a+1},$$

поэтому $f(a)=\pi\ln(a+1)+C$. Кроме того, $f(0)=0$ (замена $x=1/y$ в интеграле).

Upd. Лучше было взять $\displaystyle I(a)=\int_0^{+\infty}\frac{\ln(1+a^2x^2)}{1+x^2}\,\mathrm{d}x$: тогда не возникло бы проблем с вычислением $f(0)$.

[NSKuber]

RIP
Насколько мне известно, задумывалась замена $x=\tg y$. Дальше просто.

[RIP]

Блин, не узнал стандартный интеграл $\int_0^{\pi/2}\ln\sin x\,\mathrm dx$. Пора на пенсию.
Вообще, есть ощущение, что где-то на форуме я это уже видел.

[mihiv]

ДЛЯ ВУЗОВ НЕМАТЕМАТИЧЕСКОГО ПРОФИЛЯ
5.
Из уравнения следует: $f(0)=0\qquad (1).$Умножим уравнение на $x$ и введем новую функцию $g(x)=xf(x)$. Получим уравнение для $g(x): g(2x)-g(x)=x^3.\qquad (2)$
В уравнении (1) будем брать аргумент равным последовательно: $x, \frac x2,\frac x{2^2},\dots \frac x{2^k}$ и т.д. Просуммируем полученные уравнения по $k$ от 0 до $\infty $. В результате получим с учетом (1): $g(2x)=\frac 87x^3$. Отсюда $g(t)=\dfrac {t^3}7$ и $f(t)=\dfrac {g(t)}t=\dfrac {t^2}7$.

[TR63]

bot в сообщении #1063891 писал(а):

4. Числа $a,b,c$ являются длинами сторон некоторого треугольника. Докажите,что

$$\frac{ a }{ b+c-a }+\frac{ b }{c+a - b }+\frac{ c }{a+ b-c } \geqslant 3$$

1). Неравенство достаточно доказать для $a^2+b^2+c^2\ge3$.
2) Используя известное неравенство, следующее из неравенства К-Б, получим:
$\frac{a^2}{a(b+c-a)}+\frac{b^2}{b(c+a-b)}+\frac{c^2}{c(a+b-c)}\ge\frac{(a^2+b^2+c^2)^2}{ab+bc+ac-(a^2+b^2+c^2)}$
Сделаем обозначение $t=a^2+b^2+c^2$. Тогда будет верно неравенство (с учётом, что ($ab+bc+ac\le2(a^2+b^2+c^2)$):
$t^2+3t-6t\ge0$. Чтд.

[Sergic Primazon]

bot в сообщении #1063891 писал(а):

4. Числа $a,b,c$ являются длинами сторон некоторого треугольника. Докажите,что

$$\frac{ a }{ b+c-a }+\frac{ b }{c+a - b }+\frac{ c }{a+ b-c } \geqslant 3$$

$a=x+y $ , $b=y+z$ , $c=z+x$

$\Leftrightarrow \frac{1}{2}(\frac{x}{y}+\frac{y}{x})+\frac{1}{2}(\frac{y}{z}+\frac{z}{y})+\frac{1}{2}(\frac{z}{x}+\frac{x}{z}) \ge 3$