Численное дифференцирование непериодической функции

[Fgolm]

Здравствуйте!
Дана функция одной переменной.
Как известно, формула для вычисления производной функции на равномерной сетке по двум соседним точкам обладает весьма большой погрешностью:
$y'\left( {x_0 } \right) = \frac{{y\left( {x_1 } \right) - y\left( {x_0 } \right)}}{{\Delta x}}$
Если организуется какой-то итерационный процесс, внутри которого приходится вычислять производные, то лучше (с целью обеспечения сходимости) пользоваться другими формулами, например:
$y'\left( {x_1 } \right) = \frac{{y\left( {x_2 } \right) - y\left( {x_0 } \right)}}{{2\Delta x}}$
или т.н. первой формулой Рунге:
$y'\left( {x_2 } \right) = \frac{4}{3}\frac{{y\left( {x_3 } \right) - y\left( {x_1 } \right)}}{{2\Delta x}} - \frac{1}{3}\frac{{y\left( {x_4 } \right) - y\left( {x_0 } \right)}}{{4\Delta x}}$
Но эти формулы напрямую не позволяют вычислять производные в крайних узлах сетки.
Если процесс периодический (допустим переменная, по которой берётся производная - это время), то проблема при вычислении производной в крайних узлах отпадает.
Если процесс непериодический, то в крайних узлах можно вычислять производные по двум соседним точкам, а в остальных узлах - по более точным формулам. Но как показывает опыт, этот способ неэффективен.
Посоветуйте, как лучше решить эту проблему

[TOTAL]

Fgolm в сообщении #1039552 писал(а):

Если процесс непериодический, то в крайних узлах можно вычислять производные по двум соседним точкам, а в остальных узлах - по более точным формулам. Но как показывает опыт, этот способ неэффективен.
Посоветуйте, как лучше решить эту проблему

В крайних узлах можно вычислять производные по 3 соседним точкам. По 4 соседним точкам. Все точнее и точнее.

[Fgolm]

TOTAL в сообщении #1039723 писал(а):

В крайних узлах можно вычислять производные по 3 соседним точкам. По 4 соседним точкам. Все точнее и точнее.

Тогда производная вычисленная в крайнем узле будет равна производной, вычисленной в соседнем узле.

[ewert]

Fgolm в сообщении #1039934 писал(а):

Тогда производная вычисленная в крайнем узле будет равна производной, вычисленной в соседнем узле.

Не будет.

Нет вообще никаких "формул Рунге" -- есть лишь тупо результаты дифференцирования интерполяционного многочлена с последующей подстановкой. Чем больше брать узлов интерполирования, тем выше точность и выйдет.

[Fgolm]

Пусть имеется $n + 1$ узлов.
Вычислим производную в узле под номером 1 по трём точкам:
$y'_1 = \frac{{y_2 - y_0 }}{{2\Delta x}}$
Как будет выглядеть производная в узле под номером 0, если значение в узле -1 неизвестно, поскольку функция непериодическая?

[worm2]

Интерполируйте (или, если известно, что функция с погрешностью, аппроксимируйте) Вашу функцию сплайном третьей степени, например. И от него берите производную, хоть вторую.

[ewert]

Fgolm в сообщении #1040060 писал(а):

Как будет выглядеть производная в узле под номером 0,

$y'_0 = \frac{{-y_2+4y_1 - 3y_0 }}{{2\Delta x}}$

[Fgolm]

ewert, поясните

[INGELRII]

$y_0=y_0, y_1=y_0+y`_0 \Delta +0.5 y``_0 \Delta ^2, y_2=y_0+2 y`_0 \Delta +2 y``__0 \Delta ^2$. Будем искать производную в нуле в виде линейной комбинации $y`_0=c_0 y_0+ c_1 y_1+ c_2 y_2$. Дальше подсказки требуются?

Метод обобщается на приближения более высокой точности, с большим количеством точек.

[Someone]

Fgolm в сообщении #1039552 писал(а):

Если процесс непериодический, то в крайних узлах можно вычислять производные по двум соседним точкам, а в остальных узлах - по более точным формулам. Но как показывает опыт, этот способ неэффективен.
Посоветуйте, как лучше решить эту проблему

Собственно, один совет Вам уже дали: построить интерполяционный полином и дифференцировать его. Единственное, к чему надо относиться осторожно — это к увеличению числа узлов. Вот пример с интерполяцией функции $f(x)=\frac 1{1+100x^2}$ на отрезке $[0;2]$ по 11 точкам (с шагом $0{,}2$) полиномом 10 степени

Вложение:

Poly10.gif [ 4.39 Кб | Просмотров: 5956 ]

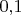
и по 21 точке (с шагом $0{,}1$) полиномом 20 степени

Вложение:

Poly20.gif [ 4.48 Кб | Просмотров: 5956 ]

Сверху — графики функции и интерполяционного многочлена (на отрезке $[1{,}5;2]$), снизу — графики их производных.
Наглядно видно, что вблизи правого конца отрезка с увеличением числа узлов погрешность интерполяции и самой функции, и её производной увеличилась, несмотря на двукратное уменьшение шага.

Другой совет тоже дали: использовать формулу Тейлора. Только лучше это сделать аккуратнее. Я буду писать $y_i$ вместо $f(x_i)$ и $h$ вместо $\Delta x$.
Пусть у нас есть три равноотстоящие точки $x_0,x_1,x_2$ с шагом $h$. Записывая формулу Тейлора в этих точках, получим

$$f(x)=f(x_i)+\frac{f'(x_i)}{1!}(x-x_i)+\frac{f''(x_i)}{2!}(x-x_i)^2+o\left((x-x_i)^2\right),\quad i=0,1,2,$$

то есть,

$$f(x)=y_i+y'_i(x-x_i)+\frac{y''_i}2(x-x_i)^2+o\left((x-x_i)^2\right),\quad i=0,1,2.$$

Далее, например, для $i=0$, подставляем $x=x_0,x_1,x_2$ и получаем систему равенств

$$\begin{cases}y_0=y_0,\\y_1=y_0+y'_0h+\frac{y''_0}2h^2+o(h^2),\\y_2=y_0+2y'_0h+2y''_0h^2+o(h^2).\end{cases}$$

Первое равенство тривиальное, а из двух других нужно исключить $y''_0$. Для этого второе равенство умножаем на $4$ и вычитаем третье: $4y_1-y_2=3y_0+2y'_ih+o(h^2)$, откуда

$$y'_0=\frac{-3y_0+4y_1-y_2}{2h}+o(h),$$

что согласуется с тем, что написал ewert.

Аналогично получаются формулы для $y'_1$ и $y'_2$, а также формулы при большем числе точек.

[ewert]

Fgolm в сообщении #1040096 писал(а):

ewert, поясните

Смысл? Откройте же наконец любую книжку по численным методам.

Someone в сообщении #1040144 писал(а):

$$y'_0=\frac{-3y_0+4y_1-y_2}{2h}+o(h),$$

Запись плохая: надо не $o(h)$, а $O(h^2)$. Поскольку речь не об анализе, а о вычислительной математике -- разница довольно принципиальна.

[Fgolm]

Someone, спасибо!

[Someone]

ewert в сообщении #1040148 писал(а):

Запись плохая: надо не $o(h)$, а $O(h^2)$.

Если функция имеет непрерывную третью производную.

[ewert]

Someone в сообщении #1040204 писал(а):

Если функция имеет непрерывную третью производную.

Достаточно ограниченности, но не в этом дело. Это в анализе достаточно абы каких оценок -- лишь бы давали качественный результат. Здесь же результаты нужны количественные, потому и оценки требуются квалифицированные.

[Someone]

ewert в сообщении #1040207 писал(а):

Достаточно ограниченности

Да.

ewert в сообщении #1040207 писал(а):

Здесь же результаты нужны количественные, потому и оценки требуются квалифицированные.

Если гладкость функции недостаточная, погрешность формулы растёт. В том числе и вместо $O(h^2)$ легко может получиться $o(h)$. А если и второй производной нет, то ещё хуже. А я не помню, чтобы гладкость функции где-то в теме указывалась.

Но если нужны количественные оценки погрешности, то с самого начала вместо $o(h^2)$ нужно писать остаточный член в соответствующей форме. Или получать оценки каким-то другим способом.