Порекомендуйте, пожалуйста, хорошую учебную литературу (на русском), где бы были введены выделенные термины:
Theorem. Let

with
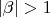
be an
algebraic number. Then

is SRZ (or WRZ) if and only if it has no
conjugate of modulus 
.
It is fairly easy to recognize whether an algebraic number does, or does not have a conjugate of modulus 1, by looking at its
minimal polynomial. First, if the number is
quadratic, it cannot have any conjugate of modulus 1. Suppose now that

is an algebraic
number of degree 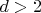
, with a conjugate
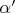
with modulus
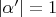
.
<...>



