Попытка самостоятельно ввести последовательность
https://oeis.org/draft/A257316Виновата, забыла, как вводить параметр offset. Я хорошо помню его назначение, но плохо знаю, как он работает.
При вводе написала offset 1,5 (это ошибка! как я сейчас поняла, правильно offset 5,1)
Система offset 1,5 не поняла и исправила на offset 1,1
Далее пошли длинные и нудные объяснения с редактором по поводу этого параметра

Объяснения осложняются ещё моим незнанием языка, то есть каждую фразу я должна переводить в Гугле и переводить свой ответ.
Я написала, что не понимаю работу параметра offset. Меня посылают сюда:
https://oeis.org/eishelp2.html#RZЯ вижу это:
Цитата:
• This line usually gives the subscript of the first term in the sequence.
o For example: the Fibonacci numbers F(0), F(1), F(2), ... begin 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,... and the subscript of the initial term is 0,
so the "Offset" line is 0
• If the sequence gives the decimal expansion of a constant, the offset is the number of digits before the decimal point.
o For example, the speed of light is 299792458 (m/sec), giving the sequence 2,9,9,7,9,2,4,5,8, with offset 9 .
• In the internal format, there is a second offset, which says which term (counting from the left, and starting with 1), first exceeds 1 in absolute value. This is set to 1 if all the terms are 0 or +-1.
Конечно, я могу начинать долго и нудно переводить это в Гугле. Но... не буду!
Я пишу следующее:
Код:
for ultra magic square of order 5 - a (x) = 3505
for ultra magic square of order 6 - a (x + 1) = 990
for ultra magic square of order 7 - a (x + 2) = 4613
for ultra magic square of order 8 - a (x + 3)=2040
Я понятно объяснила, какая у меня последовательность или не очень?
Тут пришёл
maxal и изменил параметр offset на правильный.
Жду развития событий. Последовательность пока не утверждена.
Да, интересный вопрос: какая разница между
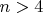
и


Мной было написано:
Цитата:
Ultra magic squares exist for orders n>4.
Исправлено редактором на:
Цитата:
Ultra magic squares exist for orders n>=5.
Как известно, порядок магического квадрата

является числом натуральным, причём

.



