Если сделать с суммированием, получится так:

Замечательное рассуждение. Если бы Вы сразу привели это неравенство, то мне бы незачем было вспоминать об интегралах. Это ясно.
Что касается суммы синусов (да и косинусов), то их неограниченность уже следует из неограниченности модуля суммы экспонент. Например так.
Положим

. Мы только что видели, что можно так подобрать

, чтобы

. Рассмотрим аргумент

. Если мы можем выбрать

так, чтобы он был отделен от углов вида

, то отсюда будет следовать соразмерность вещественной и мнимой части

. А это как раз и есть суммы синусов и косинусов. Мы сейчас покажем, что для всякого

можно выбрать

так, чтобы величина

"повернулась" на некий "фиксированный" угол. В результате мы сможем отделить аргумент от

.
Согласно теории цепных дробей найдутся сколь угодно большие

такие, что

Умножая

на степень двойки (если потребуется), отсюда легко получаем, что найдутся сколь угодно большие

такие, что

где

.
Пусть

уже как-то выбрано. Рассмотрим

. Тогда

. Значит выбирая

достаточно большим (по сравнению с

) получим, что

. А что с аргументом? Имеем

Если произведение

- четное, то

"повернется" примерно на

. Если произведение нечетное, то будет еще добавочный угол
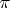
. Теперь вспоминаем условия на
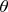
. Как бы там ни было, но от углов вида

отстроиться можно.
-- Вт апр 07, 2015 11:41:07 --Небольшое уточнение.
Там будет неравенство

.
Так что угол может быть и положительным и отрицательным. Но нам это не мешает.



