Здравствуйте, участники форума. У меня возникла вот такая задача : классифицировать конечные подгруппы в группе

. Группа

действует на

перестановкой компонент. При это мне известны все конечные подгруппы (с точностью до изоморфизма) у группы

:

, где

- циклическая группа порядка

, а

- группа диэдра порядка

.
Для начала я хотел разобраться с конечными подгруппами прямого произведения

. Пусть

- конечная подгруппа. Рассмотрим отображения :

,

- проекции. Тогда

- конечные подгруппы в проективной группе. Тогда получаем, что

, где
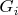
одна из

. Получается, что нужно разобрать с подгруппами прямого произведения. Сложность в том, что подгруппы произведения это не просто произведения подгрупп компонент. Есть такое утверждения - лемма Гурса
http://en.wikipedia.org/wiki/Goursat's_lemma . С помощью которой, вроде, можно находить подгруппы произведения, зная подгруппы

и

. Я не понимаю как нужно это делать. Я разобрался со случаем, когда

- циклические. Меня вот интересует, когда порядок произведения уже немаленький (просто когда маленький я уже в ручную строю произведения и смотрю на ее подгруппы). Например, вот как можно описать все подгруппы

?
И еще, я вот не совсем понимаю. Вот

действует перестановкой компонент. Отсюда же не следует, что в прямом произведении нам нужно брать только группы вида

и

?



