Задание: Пусть

- положительное число, не являющееся точным квадратом целого числа и
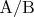
сечение в рациональных числах

. Доказать, что в

нет наибольшего, а в

наименьшего.
Может быть я что-то не понимаю, но

не является точным квадратом целого числа, но является точным квадратом рационального числа, а следовательно является наибольшим в

или наименьшим в

.