самосопряжённость именно

Нет:
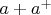
и

.
эрмитов оператор
Математики обычно считают, что эрмитов = ограниченный и симметричный. А если говорить о неограниченных операторах с областью

, то симметричный это такой, что

(т.е.

для всех

, а вот самосопряженный

. Проверка самосопряженности может быть очень сложным делом. Только для них. а не просто симметрических, есть эволюция, спектральное разложение, функция от оператора.
И не всякий симметрический оператор

имеет самосопряженное расширение

:

(см преобразование Кэли, индексы дефекта).
И тут проблемка: если мы не знаем что

, то

не будет сопряженным к

и

не будет обязательно самосопряженным (но для конкретных

и

из перевранной задачи будет).