Элементарное и истинное доказательство
Великой теоремы. Великая теорема Ферма гласит: «Ни куб на два куба, ни квадрато-квадрат и вообще никакая, кроме квадрата, степень не может быть разложена на сумму двух таких же. Я нашёл удивительное доказательство этому, однако ширина полей не позволяет здесь его осуществить».
Данная теорема утверждает, что уравнение
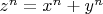
имеет решение для натуральных чисел только при

.
Решение данного уравнения в натуральных числах дает нам бесконечное множество так называемых пифагоровых троек.
Нахождение пифагоровых троек методом Евклида, согласно теореме:
Взаимно простые числа

, из которых

четно, удовлетворяют уравнению

тогда и только тогда, когда

Где

и из чисел

и

одно четно, а другое нечетно. При этом если пифагорова тройка имеет наибольший общий делитель, то она сокращается на него.
Однако, известно, что сам Пифагор находил свои тройки посредством уравнения:
Уравнение 1:

Вопрос: откуда Пифагор пришел к данному уравнению и почему, используя его, пришел к мысли что «Всё есть число»?
Возьмем произвольную окружность радиусом равным значению

, и на этом радиусе построим прямоугольный треугольник:
Рисунок 1:
URL=http://www.radikal.ru]

[/URL]
Из рисунка видно, что

Поскольку радиус окружности может принимать размерность от 1 до

, то и значения

и

, могут принимать те же значения. Для любой окружности радиусом

, всегда

. При этом, если мы рассматриваем, что

числа натуральные, то и значение

, всегда будет числом натуральным, что обеспечивает нахождение всего множества пифагоровых троек.
Представим уравнение

в виде

преобразуя которое, получим:
Уравнение 2.

Отсюда видно, что при

, мы получим искомое уравнение 1. Дальнейшие преобразования дадут:
Уравнение 3:

Уравнение 4.

Уравнения 5 и 5*.


Из этого также следует, что, придавая

значения от 1 до

, мы можем получить все бесконечное множество пифагоровых троек. Причем все эти тройки будут теперь находиться в функциональной зависимости от значений

и, таким образом, они уже не будут хаотично разбросаны.
Из этого следует, что уравнения 1 ÷ 5 являются единственными универсальными уравнениями, обеспечивающими нахождение значений

необходимых для решения уравнения

в натуральных числах.
Возьмем уравнение:

где

и представим его в виде:

Условимся, что

;

;

; тогда уравнение примет вид:

Вместо

и

подставим их значения согласно уравнениям (2), (3), которые являются единственно истинными для определения пифагоровых троек:

После возведения в степень и сокращений получим:



таким образом, данное уравнение имеет нулевое решение только когда:

и

т.е.

; и

Но такие равенства возможны только в случае, когда:

И тогда уравнение

приобретает вид:

где

что соответствует всем примитивным тройкам, умноженным на


Вывод: Если

т. е.

, то всегда

Вопрос: разве Пьер Ферма не мог записать данное доказательство на полях «Арифметики» Диофанта, или он его не знал? Знал, конечно. Только это доказательство никак не раскрывает всех тайн пифагоровых чисел и их функций. А, потому остается непонятным, почему значения

и

функционально зависят от значений

и

. И только таблично - графический анализ пифагоровых чисел и их функций приводит как к доказательству Великой теоремы методом подъема, так и к пониманию физической сущности чисел.
Полное доказательство Великой теоремы с выводами находится здесь:
http://axtezius.ucoz.ru/С уважением: Н. Акс