Вопрос № 2. Производная и средняя скорость: продолжениеКак и прежде, назовем средней скоростью изменения функции на отрезке
![$[a, b]$ $[a, b]$](https://dxdy-04.korotkov.co.uk/f/b/d/4/bd4455e79810acc06e3d31c60fb8bfb282.png)
величину

.
В прошлый раз мы доказали такое утверждение. Пусть функция

дифференцируема во внутренней точке своей области определения

. Рассмотрим последовательность

, сходящуюся к

, и последовательность

, сходящуюся к

, причем для любого

верно

. Тогда последовательность

, где

есть средняя скорость изменения функции на участке
![$[a_i, b_i]$ $[a_i, b_i]$](https://dxdy-03.korotkov.co.uk/f/6/2/0/620589dfeb9a91d651911f6ae0d97bb482.png)
, сходится к

.
Теперь хочется доказать обратное утверждение и тем самым установить, что производная есть в точности предел средней скорости. А именно, пусть

- внутренняя точка области определения функции. Пусть для любых последовательностей

и

сходящихся к

, причем для любого

верно

, последовательность

, где

есть средняя скорость изменения функции на участке
![$[a_i, b_i]$ $[a_i, b_i]$](https://dxdy-03.korotkov.co.uk/f/6/2/0/620589dfeb9a91d651911f6ae0d97bb482.png)
, сходится к числу

. Доказать, что тогда функция дифференцируема в точке

, причем

.
Пытаюсь доказать. Возьмем произвольную последовательность

, сходящуюся к

, но не содержащую его. Требуется доказать, что

. Может встретиться три ситуации:
1)

сходится к

слева
2)

сходится к

справа
3)

можно разбить на две на две подпоследовательности -

, сходящуюся к

слева, и

, сходящуюся к

справа.
Итак, если мы докажем, что для произвольной последовательности

, сходящейся к

слева или справа, верно

, мы докажем утверждение теоремы.
Все значительно упростилось бы, если бы верным оказалось такое утверждение: «Пусть для любых последовательностей

и

сходящихся к

, причем для любого

верно

, последовательность

, где

есть средняя скорость изменения функции на участке
![$[a_i, b_i]$ $[a_i, b_i]$](https://dxdy-03.korotkov.co.uk/f/6/2/0/620589dfeb9a91d651911f6ae0d97bb482.png)
, сходится к числу

. Тогда для любых последовательностей

и

сходящихся к

, причем для любого

верно

, но

и
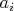
никогда не равны

одновременно, последовательность

, где

есть средняя скорость изменения функции на участке
![$[a_i, b_i]$ $[a_i, b_i]$](https://dxdy-03.korotkov.co.uk/f/6/2/0/620589dfeb9a91d651911f6ae0d97bb482.png)
, сходится к тому же самому числу

». Будь это утверждение верным, мы бы просто применили его к последовательности

, взяв в качестве парной стационарную последовательность

. Но, увы, такое утверждение неверно - пример дается функцией с устранимым разрывом в точке

. Выносить же в условие непрерывность функции не хочется, ибо цель и состоит в том, чтобы доказать, что существования конечного предела у средней скорости достаточно для дифференцируемости, не говоря про непрерывность.
В общем, я снова прошу меня пнуть.



