отображение определено как сопоставляющее правило.
А это то же самое. Только пользоваться таким определением очень неудобно. Особенно при решении теоретико-множественных задач.
мне тоже сначала так показалось
Не знаю, что вам показалось. Но использованное в решении выражение

в точности означает, что

. Никакого другого смысла оно не несет.
поэтому и понадобилась помощь по этой задаче.
Возможно здесь помощь требуется составителям задач?

Правильно ли я понял, что отображение
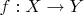
должно ставить в соответствие какой-то

обязательно любому

?
Разумеется.
Т.е. если хоть какой-то

"остается на месте", то это уже не будет отображением из

?
Если хоть какой-то элемент

не находит своего образа в множестве

, то в лучшем случае мы имеем частичную функцию. Но даже частичная функция — не функция.

А вот в множестве

напротив могут быть элементы, в которые никакие

не переходят?
Лучше не используйте слово "переходят", оно вас сбивает. В множестве

действительно могут быть элементы, которые не имеют прообраза в

, при этом говорят, что функция не является сюръекцией. Но в общем случае от функции выполнение этого условия и не требуется.
И если так, то получается любое отображение типа

можно обозначить скажем как

или

?
Нет, с точки зрения стандартного определения это разные отображения.
если какой-то

переходит в 2 разных

, то это не отображение?
Нет. В лучшем случае это "многозначная функция", то есть другое совершенно понятие.



