Устранил описки в тексте сообщения.
Рассмотрю метод оценки количества решений диофантовых уравнений - Круговой метод Харди-Литлвуда (КМ). Данный метод позволяет определить количество решений диофантовых уравнений без нахождения самих решений. Круговой метод Харди-Литлвуда может быть использован для получения количества решений далеко не всех уравнений, но позволяет сделать достаточно точно. КМ позволяет определить асимптотику количества решений для некоторых типов алгебраических диофантовых уравнений.
Если рассматривать алгебраическое диофантово уравнение:

, (1)
то если все коэффициенты целые и положительные и

целое и положительное, то уравнение (1) имеет конечное число неотрицательных или натуральных решений (в случае отсутствия решений считается, что количество решений равно 0, т.е. также конечно). В случае конечного числа решений КМ дает асимптотику количества решений уравнения (1) в зависимости от значения

.
Обозначим

- соответственно количество неотрицательных и положительных целых (натуральных) решений уравнения (1).
Так как

являются последовательностями, то для них существуют производящие функции соответственно:

, (2)

, (3)
если указанные ряды сходятся при

.
Поговорим о получении производящих функций (2), (3):

,

.
Рассмотрим количество натуральных решений уравнения:

, (4)
где все
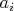
- нутуральные числа и

.
Известно, что данное уравнение имеет натуральные решения, если

кратно наибольшему делителю
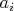
. В остальных случаях

.
Получим производящую функцию количества натуральных решений уравнения (4):

. (5)
Так как все ряды в (5) сходятся при

, то получим:

. (6)
Аналогично (6) получим производящую функцию количества неотрицательных решений уравнения (4):

. (7)
Так как все ряды в (7) сходятся при

, то получим:

. (8)
В частном случае на основании (6), (8) получим производящие функции количества решений для уравнения:

, (9)
где

.
Производящая функция количества натуральных решений уравнения (9) на основании (6):

. (10)
Аналогично (10) производящая функция количество неотрицательных решений уравнения (9) на основании (8):

. (11)
Обозначим аналитическое продолжение производящих функций (2), (3) на комплексную область

соответственно:

(12).
Если функции (12) являются аналитическими в области

, то их можно почленно дифференцировать в этой области нужное число раз и на основании теорем Коши и Тейлора (ТФКП) справедливы формулы:
![$R_s(n)=Res[\varphi(z)/z^{n+1},0]=1/n!\lim_{z \to 0} \varphi^{(n)}(z)=1/2\pi i\int_{|z|<R}{\varphi(z) dz/z^{n+1}$ $R_s(n)=Res[\varphi(z)/z^{n+1},0]=1/n!\lim_{z \to 0} \varphi^{(n)}(z)=1/2\pi i\int_{|z|<R}{\varphi(z) dz/z^{n+1}$](https://dxdy-02.korotkov.co.uk/f/d/f/6/df63282359d2403b61f4a7929fafcace82.png)
, (13)
![$R_s^{+}(n)=Res[\varphi^{+}(z)/z^{n+1},0]=1/n!\lim_{z \to 0}\varphi^{+(n)}(0)=1/2\pi i\int_{|z|<R}{\varphi^{+}(z) dz/z^{n+1}$ $R_s^{+}(n)=Res[\varphi^{+}(z)/z^{n+1},0]=1/n!\lim_{z \to 0}\varphi^{+(n)}(0)=1/2\pi i\int_{|z|<R}{\varphi^{+}(z) dz/z^{n+1}$](https://dxdy-02.korotkov.co.uk/f/d/c/8/dc859a55ced62e70b3a27544d596509e82.png)
. (14)
Отсюда в честь авторов и название метода - Круговой метод Харди-Литлвуда.
Так как производящие функции (6), (8) являются аналитическими при

, то на основании (13), (14) для количества решений уравнения (4) справедливы формулы:

. (15)

.(16)
Так как производящие функции (10), (11) являются аналитическими при

, то на основании (13), (14) для количества решений уравнения (9) справедливы формулы:

. (17)

. (18)
Интегралы (15) - (18) можно находить с помощью вычетов для получения количества решений уравнений (4), (9) при небольших значениях

.
Например, найдем количество решений для уравнения типа (9):

. (19)
На основании формулы (18) для уравнения (19) получаем количество неотрицательных решений:
![$$R_5(1)=1/2\pi i\int_{|z|<1}{dz/z^{2}(1-z)^{5}}=Res[1/z^2(1-z)^5,0]=\lim_{z \to 0}((1-z)^{-5})'}=5$$ $$R_5(1)=1/2\pi i\int_{|z|<1}{dz/z^{2}(1-z)^{5}}=Res[1/z^2(1-z)^5,0]=\lim_{z \to 0}((1-z)^{-5})'}=5$$](https://dxdy-02.korotkov.co.uk/f/5/9/9/5997ae3b634a6055f8a3c51007f2d42282.png)
На основании формулы (17) для уравнения (19) получаем количество натуральных решений:

, так как интеграл берется от аналитической функции.
Теперь найдем количество решений для уравнения типа (4):

. (20)
На основании формулы (15) для уравнения (20) получаем количество натуральных решений:
![$R_2^{+}(5)=1/2\pi i\int_{|z|<1}{z^{5}dz/z^{6}(1-z^{3})(1-z^{2})}$=Res[1/z(1-z^3)(1-z^2),0]=\lim_{z \to 0}{1/(1-z^3)(1-z^2)}=1$ $R_2^{+}(5)=1/2\pi i\int_{|z|<1}{z^{5}dz/z^{6}(1-z^{3})(1-z^{2})}$=Res[1/z(1-z^3)(1-z^2),0]=\lim_{z \to 0}{1/(1-z^3)(1-z^2)}=1$](https://dxdy-03.korotkov.co.uk/f/e/5/9/e5906789fdad94b25d2c44a4dbf55d5d82.png)
На основании формулы (16) для уравнения (20) при вычислении количества неотрицательных решений получаем:
![$R_2(5)=1/2\pi i\int_{|z|<1}{dz/z^{6}(1-z^{3})(1-z^{2})}=Res[1/z^{6}(1-z^{3})(1-z^{2}),0]$ $R_2(5)=1/2\pi i\int_{|z|<1}{dz/z^{6}(1-z^{3})(1-z^{2})}=Res[1/z^{6}(1-z^{3})(1-z^{2}),0]$](https://dxdy-04.korotkov.co.uk/f/3/7/1/3715eadd9e3cabb023b6ae0ed2ceff7b82.png)
. (21)
Таким образом, при вычислении (21) для сравнительно небольших значений

мы сталкиваемся с трудностью вычисление значения вычета в полюсе 6 порядка. В общем случае при больших значениях

метод вычисления интегралов (15) - (18) через вычеты не подходит, поэтому требуется асимтотическая оценка по

указанных интегралов сверху.
Оценка количества натуральных и неотрицательных решений для уравнения (9) известна, поэтому рассмотрим более сложные случаи.
Рассмотрим уравнение:

, (22)
где все

- неотрицательные числа, а

-большое натуральное число.
Уравнение (22), в отличие от (9), имеет решения не при всех значениях

. Не будем останавливаться на условиях существования решений для уравнения (22). Для нас важно, что количество неотрицательных решений в случае их отсутствия равно 0. Нам нужно найти асимптотику количества неотрицательных решений уравнения (22) в случае, если решение этого уравнения существует.
Харди и Литлвуд с помощью своего метода нашли асимптотику количества представлений числа

при

:

, (23)
где

-гамма функция,

-сумма ряда,

- малое положительное действительное число.
Для определения количества неотрицательных решений уравнения (22) надо количество представлений, полученное по формуле (23) умножить на возможное количество перестановок переменных

:

. (24)
Позднее Виноградов, развив метод Харди-Литлвуда, доказал, что (23) справедливо уже при

.
При этом при

значение

, а при

значение

, где

- малое положительное действительное число.
Кроме того доказано, что

при

,

, если

и является степенью 2, а также при

в остальных случаях.
Проанализируем формулу (23).
Минимальное значение

для уравнения (22) получается при
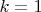
.
Асимптотику количества неотрицательных решений данного уравнения для

формула (23) не определяет.
Максимум количества решений по формуле (23) достигается естественно при
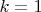
. В этом случае на основании (24) получаем:

. (25)
При

на основании вышесказанного

в формуле (23), что не дает оценку сверху.
Однако, известно, что ряд сходится абсолютно, поэтому

. Учитывая, что при

значение

, то в в этом случае справедлива оценка:

. (26)
Однако, оценка (26) не точная, поэтому формула (24) интересна при

.
В этом случае,на основании (24), асимптотическая оценка количества решений уравнения (22):

. (27)
В случае

требуется отдельная оценка, которой мы займемся.
Виноградов получил следующую формулу для определения количества представлений числа

, как сумму

степеней неотрицательных чисел:

, (28)
где
![$f(x)= \Sigma_{m=1}^{[n^{1/k}]} {e^{2\pi x m^k}}$ $f(x)= \Sigma_{m=1}^{[n^{1/k}]} {e^{2\pi x m^k}}$](https://dxdy-02.korotkov.co.uk/f/1/2/1/12115c7b5b2638769be76765c28f876282.png)
, (29)
а
![$[A]$ $[A]$](https://dxdy-02.korotkov.co.uk/f/5/4/6/5466ebcb58608f2abe3081afb6a905d682.png)
- целое значение числа

.
Известна лемма Хуа (Р. Вон "Метод Харди-Литлвуда", М, Мир, 1988, 184, стр 20):
Пусть

. Тогда

, где
![$N=[n^{1/k}]$ $N=[n^{1/k}]$](https://dxdy-02.korotkov.co.uk/f/1/6/a/16a7369fbad95f4943d40e133dba127d82.png)
, а

- малое действительное положительное число.
Для

на основании леммы Хуа получим:

. (30)
Для

воспользуемся неравенством Коши-Буняковского (Шварца):

. (31)
На основании леммы Хуа и (31) получим оценку:

. (32)
Для

на основании леммы Хуа получим:

. (33)
Формулы (30),(32),(33) значительно лучше тривиальной оценки:

.
Для определения количества неотрицательных решений уравнения (22) надо количество представлений, полученное по формулам (30),(32),(33) умножить на возможное количество перестановок переменных

:

. (34)
Теперь рассмотрим верхнюю оценку количества неотрицательных решений уравнения:

, (35)
где все

- неотрицательные числа, все
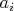
- натуральные, а

-большое натуральное число.
Верхняя оценка количества решений уравнения (35) при больших

равна:

, (36)
т.е равна верхней оценке количества неотрицательных решений уравнения (22) при больших

, деленной на произведение коэффициентов уравнения (35).
Это связано с тем, что при переборе вариантов решений значение переменной

в уравнении (35) меняется с шагом равным значению
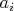
, т.е. общее количество шагов перебора вариантов решения уменьшается на произведение коэффициентов уравнения (35) по сравнению с количеством шагов перебора для уравнения (22).
Теперь рассмотрим уравнение:

, (37)
где

-натуральные числа, такие что:

и

. (38)
Мы не будем рассматривать вопросы разрешимости данного уравнения в неотрицательных числах. Это вопрос заслуживающий отдельного обсуждения.
Нас будет интересрвать только верхняя оценка количества решений данного уравнения в неотрицательных числах, когда такие решения существуют, так как если уравнение (37) не разрешимо в неотрицательных числах, то количество его решений равно 0.
Сначала сделаем предварительную верхнюю оценку количества неотрицательных решений уравнения (37).
Следуя Вону и Виноградову можно записать, что количество неотрицательных решений уравнения (37) равно:

,(39)
где
![$f_i(x)=\Sigma_{m=1}^{[n^{1/k_i}]}{e^{2\pi xm^{k_i}}}$ $f_i(x)=\Sigma_{m=1}^{[n^{1/k_i}]}{e^{2\pi xm^{k_i}}}$](https://dxdy-04.korotkov.co.uk/f/f/3/2/f3257a1760a6a1aca31177e17a97d5c282.png)
. (40)
На основании (39):

, (41)
так как

.
На основании (41):

. (42)
На основании (40):
![$\max |f_i(x)|=\max |\Sigma_{m=1}^{[n^{1/k_i}]}{e^{2\pi xm^{k_i}}} | \leq \Sigma_{m=1}^{[n^{1/k_i}]}|{e^{2\pi xm^{k_i}}}|=[n^{1/k_i}]$ $\max |f_i(x)|=\max |\Sigma_{m=1}^{[n^{1/k_i}]}{e^{2\pi xm^{k_i}}} | \leq \Sigma_{m=1}^{[n^{1/k_i}]}|{e^{2\pi xm^{k_i}}}|=[n^{1/k_i}]$](https://dxdy-03.korotkov.co.uk/f/e/a/5/ea56b2b9e8cf6f809240cd096ccc2e7b82.png)
, (43)
где
![$[A]$ $[A]$](https://dxdy-02.korotkov.co.uk/f/5/4/6/5466ebcb58608f2abe3081afb6a905d682.png)
- целая часть числа

),
так как

.
Следовательно, на основании (42) и (43) мы получаем предварительную оценку:

. (44)
Смотри условие (38).
Теперь сделаем более точную верхнюю оценку количества неотрицательных решений уравнения (37).
На основании (39):

, (45)
так как

.
На основании (45) и неравенства Гельдера:



. (46)
Используя (46), лемму Хуа и обозначив

получим:


. (47)
Если преобразовать оценку (47) и сравнить с (44):


, (48)
то на основании (48) становится ясно, что оценка (47) более точная.
Теперь рассмотрим верхнюю оценку количества неотрицательных решений уравнения:

, (49)
где все

- неотрицательные числа, все
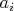
- натуральные, а

-большое натуральное число.
Верхняя оценка количества решений уравнения (49) при больших

равна:

, (50)
т.е равна верхней оценке количества неотрицательных решений уравнения (47) при больших

, деленной на произведение коэффициентов уравнения (49).
Это связано с тем, что при переборе вариантов решений значение переменной

в уравнении (49) меняется с шагом равным значению
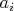
, т.е. общее количество шагов перебора вариантов решения уменьшается на произведение коэффициентов уравнения (49) по сравнению с количеством шагов перебора для уравнения (37).



