Запись

означает «повернуть репер вдоль его оси

на угол

».
Может быть "повернуть репер вокруг его оси

..."?
Это я поленился набирать фразу целиком, скопировал предыдущую, и вот результат. Конечно, вокруг оси.
Пока не понятно то, как Вы обозначили в записи движение второго относительно первого... На мой взгляд, получилось, что все три репера имеют свои углы наклона, углы поворота и радиусы относительно "нулевой" аппликаты. То есть, мы получили три независимых винтовых движения, правильно понял?
Движение получается тогда, когда мы начинаем менять параметр

. При этом начинают меняться

(линейно от времени).
Реперов здесь аж десять (а то и 11), хотя винтовых линий только три. Это потому, что я разбил построение на совершенно элементарные сдвиги и повороты. Вот, например, как получается первая винтовая линия.

Исходный репер, неподвижный.

Следующий — движется от него со скоростью

вверх. В момент

он сдвинулся на

вдоль оси

. Выше он обозначен (0).

Следующий — вращается вокруг оси

предыдущего репера с угловой скоростью

, и в момент

повернут относительно него на угол

. Но его начало отсчета находится там же.

Следующий — сдвинут на

относительно предыдущего вдоль его оси

. Но так как предыдущий вращается, то этот тоже вращается. Его начало уже находится на винтовой линии. Он движется по ней, потому что предыдущий репер тоже движется.

Следующий — повернут относительно предыдущего на постоянный угол
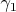
. Его начало находится там же, где и предыдущего, т.е. движется по первой винтовой линии. Вдобавок благодаря повороту его ось

направлена по касательной. Выше он обозначен (1).
И так далее.
Так получается движение. Но в каждый фиксированный момент для получения результата (точки на кривой) нужно просто проделать некоторые конкретные сдвиги и повороты.
Как видите, здесь довольно много произвольных констант. Если мы хотим рассматривать не самый общий случай, надо их конкретизировать или связать друг с другом. Некоторые связи очевидны, например,

, другие зависят от Ваших запросов.