Посмотрим, как осуществляется переход от одних координат к другим на примере сферически-симметричного коллапсирующего тела с нулевым давлением и однородным по плотности. Посмотрим также, как проводится сшивка на границе области, разделяющей вакуум и вещество. Рассмотрим вопрос, откуда берутся сингулярные решения, получим общее решение коллапса с определенными начальных данных.
В основном буду придерживаться главы Вайнберга про коллапс пар. 9 стр. 368 и ЛЛ-2 пар. 103. Обозначения буду использовать как у Ландау, хотя в некоторых местах этот вопрос лучше изложен у Вайнберга.
Я пытаюсь дополнить учебники некоторыми расчетами, которые мне показались важные для понимания классической задачи коллапса пылевого облака с нулевым давлением.
1.Координатные преобразования. Переход от стандартных координат к синхронным. Мы имеем пылевое облако с нулевым давлением в собственной системе отсчета и плотностью

постоянной во время коллапса. В координатах Шварцшильда (стандартных) это решение найдено у Вайнберга в параграфе 9 стр. 368 (ближе к концу).
Вначале там рассматривался коллапс из состояния покоя, то есть в момент времени

все частицы покоились и граница имела координату

(координата внутреннего решения) в сопутствующей СО. Полное решение включает в себя 2 области внутреннюю и внешнюю с метриками в координатах

(везде

). Но затем Вайнберг в пар. 9 получил в стандартных координатах полное решение той же задачи:

вне вещества

внутри вещества
В дальнейшем я для упрощения иногда буду опускать знаки (+) (-) , и оговаривать это, когда буду рассматривать отдельно метрику внутри и снаружи.
Внешняя метрика это стандартная метрика Шварцшильда:

,

Внутреннюю нашел Вайнберг в своей работе (Гравитация и Космология) это (11.9.31) и (11.9.32), радиальную компоненту выпишу:


- масштабный фактор. Нулевая компонента сложная и в неявном виде, выписывать не буду, впрочем, в дальнейшем мне ее явный вид не потребуется. Отмечу, что в стандартных координатах осуществлена
сшивка всех 4-х компонент внутренней и внешней метрик на границе облака! Показана их непрерывность, но не гладкость.
Теперь давайте перейдем к синхронным координатам (То есть это обратная задача, чем это описано у Вайнберга)

к

:

, через тензорный закон преобразования компонент.

Черта сверху обозначает метрику в синхронных координатах. Распишем ее компоненты для нашего случая:




Точка сверху – производная по

, штрих сверху – производная по

. Теперь, если оба выражения (1)-(2) подвергнуть преобразованиям по закону (4-7), где функции

всюду дифференцируемые, то получим решение той же модели поля в других координатах

, причем оно будет также сшито непрерывно на границе области для всех компонент, если использовать одинаковые преобразования координат, как для внутренней, так и для внешней области.
Отличительной особенностью этого решения заключается в том, что оно допустимо, когда граница облака имеет значении радиальной координаты

, то есть это означает, что мы имеем бесконечно коллапсирующий объект без всякой сингулярности, а линия

,

принадлежит нашему многообразию.
Замечание 1. Хочется также отметить одно обстоятельство, которое хорошо известно, но почему-то забывается: поскольку система уравнений (3), описывающая переход в другую координатную систему, линейна относительно старых компонент, то никаких особенностей у новых метрических компонент не должно возникнуть при допустимых преобразованиях координат, аналогично и если такая особенность имела место в старых координатах, то в новых ее нельзя устранить.
Условия синхронности:

Чтобы найти такие преобразования, мы должны решить дополнительно нелинейную систему уравнений в частных производных:


Поскольку систему (8-9)
нелинейная ( и достаточно сложная, часто не решаемая в общем виде), заранее нельзя сказать насколько гладкими получатся функции во всей области рассматриваемого многообразия. Коэффициенты в системе (8-9)

, разные во внутренней и внешней областях, значит, получим и различные функции вне

и внутри вещества

. Поэтому мне не ясно, почему два
ЗУ в одной из тем выносили мне мозг, что координатные системы внутри и снаружи пылевого облака одинаковы. Они называются одинаково: синхронные, но в сущности разные. Уже на этом этапе можно понять, что метрическая синхронная компонента ( радиальная) будет терпеть разрыв на границе облака (если граница резкая). Но далее я покажу это строго.
Выражая из (8)

и из (9)

подставим их в (5), получим:

Это выражение для радиальной компоненты в синхронных координатах в общем виде внутри и вне вещества.
Полученная геометрия выражается теперь такими метриками:

в вакууме

внутри облака
Казалось бы, если есть особенность в компоненте
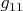
, то в (10) в

ее уже нет. На самом деле, как получил Вайнберг в параграфе 11 и в своей работе Оппенгеймер-Снайдер, преобразования

имеют сингулярность при

, когда граница облака равна

, что противоречит дифференциальной геометрии, то есть их нельзя использовать при данных условиях.
Таким образом, никакими
допустимыми преобразованиями особенность в радиальной компоненте при

устранить невозможно. (1)-(2) это есть хорошее решение без физических сингулярностей и представляет собой бесконечно (по времени

) коллапсирующий объект.
Возникает вопрос – откуда берутся решения с сингулярностями в инвариантах кривизны?
Сегодня или завтра проложу. (если есть опечатки и косяки, то пока могу исправить).