меня удивило то, что Вы не использовали классические обозначения
Во-первых, я не знаю "классическое обозначение". Если и знал, то забыл. Вам шашечки или ехать?
Во-вторых, в моих обозначениях при
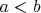
формула определяет геометрическое место точек (в форме эллипса), у которых
сумма расстояний до опорных точек равна

. Другими словами, моя формула демонстрирует не просто формальную близость гиперболы и эллипса (плюс заменяется на минус и наоборот), а смысловое единство их
определений.
В случае

эллипс вырождается в отрезок, соединяющий опорные точки.