Тест простоты
Проверим на делимость на 2,3,5
Если число имеет вид

или

тогда

Если число имеет вид
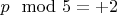
или

тогда


- число Фибоначчи
Если

mod p=0 и

mod p=1
или

mod p=0 и
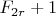
mod p=1
или

mod p=0 и

mod p=1
Число Фибоначчи вычислять через матрицы
Доказательство, если p простое, то r или 2r или 4r - период Пизано
см Википедию
Если p - составное и r период
1. Если составное число включает простые множители в степени более 1, то НОД(p,r)=p_1, но НОД(p,p-1)=1 и НОД(p,p+1)=1 значит все множители могут входить только в первой степени
2. Пусть



Число множителей p нечетное
Доказательство
рассмотрим выражение по модулю p_1
в левой части -1 в правой части все параметры не кратны p_1
Возьмем последовательно правую и левую часть по модулю p_1 p_2 .... h_1 h_2
тогда


взаимнопросты с
