Угол тета в выводе уравнения колебаний струны

[Kyogre]

Делаю курсовую по мат. анализу. Вот вырезка: http://yadi.sk/d/3zQTghRFRDPFx (лучше смотреть через сам Office, нежели через просмотрщик яндекса)
В выводе уравнения не понимаю откуда взялся угол тета (нуль с кружочком). Он на второй странице документа по центру в неравенстве и в самой формуле.
И ещё не понятно, какая часть теоремы Лагранжа была использована при выводе той формулы, где тета.

Часть вырезки в текстовом виде:
Процесс колебания струны описывается одной функцией $u (x, t)$. На концах элемента струны по касательным к струне действуют силы $T$. Пусть касательные образуют с осью $Ox$ углы $\varphi$ и $\varphi$ +\Delta\varphi. Тогда проекция на ось $Ou$ сил, действующих на элемент $MM'$, будет равна $T \sin (\varphi+\Delta\varphi) - T \sin\varphi $. Так как угол $\varphi$ мал, то можно положить $\tg \varphi \approx \sin \varphi$, и мы будем иметь:
T \sin (\varphi + \Delta\varphi) - T \sin\varphi = T \tg (\varphi + \Delta\varphi) - T \tg \varphi = T [\delta u (x+\Delta x, t)/\delta x - \delta u (x, t)/ \delta x] = T [\delta^2 u (x + \theta \Delta x, t)/\delta^2 x] \Delta x = T [\delta^2 u (x, t)/\delta^2 x] \Delta x
$0 < \theta < 1$
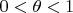
(здесь была применена теорема Лагранжа "о среднем значении" к выражению, стоящему после второго знака равно).

[Deggial]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
Причина переноса: содержание темы не приведено в теме

Kyogre
Приведите нужный для понимания текст прямо в теме. Согласно правилами оформления внешних ссылок, то, что стоит за ссылкой, должно быть необязательным для понимания существа темы.
Напоминаю, что все формулы и термы $\TeX$ом.
Инструкции по оформлению формул здесь или здесь (или в этом видеоролике).
После исправлений сообщите в теме Сообщение в карантине исправлено, и тогда тема будет возвращена.

Тема перемещена из форума «Карантин» в форум «Помогите решить / разобраться (М)»
Вернул

[ewert]

Kyogre в сообщении #867506 писал(а):

не понимаю откуда взялся угол тета

Он не угол, а просто некоторое число из интервала (как честно и сказано) от нуля до единицы.

Kyogre в сообщении #867506 писал(а):

не понятно, какая часть теоремы Лагранжа была использована при выводе той формулы, где тета

Никакая не часть, а просто сама теорема Лагранжа: отношение приращений равно производной в некоторой промежуточной точке. В данном случае приращение берётся для производной и, соответственно, в промежуточной точке производная уже вторая.

А вместо $\delta$ надо использовать $\partial$ (\partial)

[Kyogre]

Понял. А откуда взялось домножение на $\Delta x$ в последних двух выражениях?

[Munin]

На теорему Лагранжа внимательней посмотрите.