Здравствуйте, не могли бы помочь?
Есть задача: На единичной окружности (

) выбирается случайная точка

(из равномерного распределения). в единичном круге (

) выбирается случайная точка

(также из равномерного). Пусть

- прямоугольник со сторонами, параллельными осям координат и диагональю
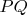
. Какова вероятность того, что весь прямоугольник лежит в круге.
У меня рассуждения такие, возьмем точку

на четверти окружности

, тогда вероятность того, что весь прямоугольник лежит в круге равна

, дальше как я понимаю нужно воспользоваться формулой полной вероятности, но я знаю формулу только для конечных наборов событий, интуитивно понятно, что нужно проинтегрировать, но как?(в интернете не нашел)