"пространство-время" требует меньше краски на печати, чем "пространство и время". Экономия и большая выгода для с/х.
Особенно по-английски, там даже на дефис не тратятся: spacetime.
-- 09.03.2014 19:27:55 --Вот он секретными письмами и убедил Лоренца с Пуанкаре не париться и писать четырёхвекторы, чтобы у них раньше времени руки не отвалились, и они смогли бы встретиться и поводить хоровод.
4-векторы ввёл всё-таки Минковский. И даже после этого, ещё долго (несколько лет) физики не вводили 4-тензоры, а пользовались более громоздкими и частными обозначениями (например, электромагнитное поле называли "6-вектором", по числу различных ненулевых компонент). Кто ввёл тензоры - точно не помню, и может быть, даже Эйнштейн (известно, что от значка
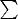
избавился именно он - по крайней мере, это носит название "нотация Эйнштейна").
-- 09.03.2014 19:42:31 --Что его вынудило или кто его вынудил?
Его вынудила математическая необходимость, если коротко. Такая же неизбежная, как та, что приводит от квадратного уравнения к формуле для его корней.
Если более полно, то оказалось, что некоторые законы физики, которые считались до этого разными, на самом деле - одни и те же законы, но "под разным углом зрения". И вот, чтобы это описать, надо было научиться "поворачивать" их под разными углами, что и требует поворотов не только в плоскостях



но и в плоскостях



- то есть, полной системы поворотов в пространстве

Это аналогично тому, как если бы вы ходили по земле вокруг зданий, и видели их повороты в плоскости

а потом представили бы себе их как пространственные объекты, на которые можно взглянуть сверху, с высоты птичьего полёта, и для этого надо было бы представить себе, как они повернутся в плоскостях

и

При этом обнаружилось, что в паре законов есть ещё и неточности, которые раньше были незаметны, и Эйнштейн их исправил. Но это другой сюжет, в данном случае менее интересный. Хотя некоторые обсуждающие пытаются тут свести разговор на другие темы, увы.
Честно говоря я не понимаю о чём Вы говорите. Какая практическая польза была в этом слиянии?
См. выше. Удобно понимать, что здание - это такая трёхмерная штука. И очень неудобно этого не понимать. Кроме того, полезно пользоваться уточнёнными законами, а не старыми ошибочными.
Так как абсолютно инерциальные системы представляют собой математическую абстракцию и в природе не существуют следует ли отсюда что теория относительности не имеет отношения к реальности?
Нет, не следует. В физике полно теорий, которые пользуются такими абстракциями, но всё равно эти теории имеют прямое отношение к реальности. Например, в механике есть абстракция материальная точка, в молекулярной теории - абстракция идеальный газ, в электричестве - абстракция неподвижный заряд, и так далее. Абстракции - это всего лишь инструмент для описания, это те "кисти", которыми физика "рисует реальность". Они приближённо описывают реальность, а не оторваны от неё напрочь.