Definition as velocities of curvesSuppose

is a

manifold (
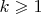
) and

is a point in

. Pick a chart
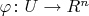
where

is an open subset of

containing

. Suppose two curves
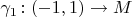
and
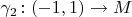
with
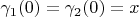
are given such that
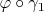
and
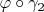
are both differentiable at

. Then
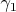
and
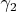
are called equivalent at

if the ordinary derivatives of
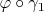
and
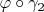
at

coincide. This defines an equivalence relation on such curves, and the equivalence classes are known as the tangent vectors of

at

. The equivalence class of the curve

is written as
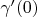
. The tangent space of

at

, denoted by
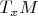
, is defined as the set of all tangent vectors; it does not depend on the choice of chart

.
To define the vector space operations on
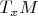
, we use a chart
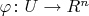
and define the map
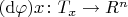
by
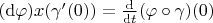
. It turns out that this map is bijective and can thus be used to transfer the vector space operations from

over to
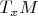
, turning the latter into an

-dimensional real vector space. Again, one needs to check that this construction does not depend on the particular chart

chosen, and in fact it does not.
Или любое из двух других определений.