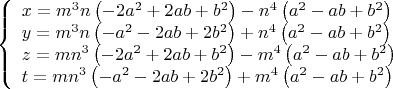Выше я рассмотрел "крайний" случай, когда

представимы формой
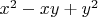
Рассмотрим другой "крайний" случай.
Если простое число вида
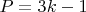
есть делитель числа
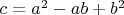
, то и

и
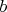
делятся на это простое число, а, следовательно,

делится на квадрат этого простого числа.
В общем случае условие

взаимно простые целые числа, содержащие только простые числа вида
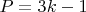
не обязательно. Но в противном случае уже нельзя утверждать, что эти формулы описывают все целые решения для данных

, поскольку простое число вида
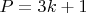
, или число 3 не обязаны делиться на

и

Итак.
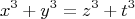
для некоторых целых чисел.
Пусть
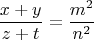
где

взаимно простые целые числа, содержащие только простые числа вида
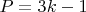
Тогда
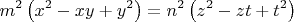
Отсюда,
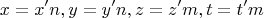
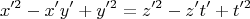
Можно показать, что это возможно только тогда, когда


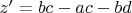

Для некоторых целых

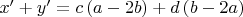
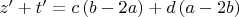
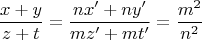
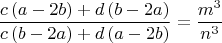
![$c\left[ {n^3 \left( {a - 2b} \right) - m^3 \left( {b - 2a} \right)} \right] = d\left[ {m^3 \left( {a - 2b} \right) - n^3 \left( {b - 2a} \right)} \right]$ $c\left[ {n^3 \left( {a - 2b} \right) - m^3 \left( {b - 2a} \right)} \right] = d\left[ {m^3 \left( {a - 2b} \right) - n^3 \left( {b - 2a} \right)} \right]$](https://dxdy-02.korotkov.co.uk/f/9/3/9/9397c6e1839ae27b648c05e507a1907e82.png)
Выберем

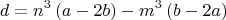
Окончательно получим