whitefox уже давал вам ответ на этот вопрос:
post644762.html#p644762Ага, так я это помню
 whitefox
whitefox и писал, как я помню, что преобразования такого в чистом виде у Россера нет, но его можно скомбинировать. Так? Или я неправильно запомнила?
Сейчас гляну

А по поводу преобразования Q что скажете?
-- Ср авг 21, 2013 09:47:36 --Правильный ответ
whitefox в этом посте:
Форма записи не моя, а Россера.

Означает, что квадрат

преобразуется в квадрат

по правилу:

В прошлом посте я ошибся, вместо преобразования Россера

нужно взять преобразование

.
Сначала применим преобразование
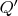
, получим матрицу индексов:
Код:
00 14 23 32 41
44 03 12 21 30
33 42 01 10 24
22 31 40 04 13
11 20 34 43 02
Теперь применим преобразование

, получим:
Код:
00 23 41 14 32
33 01 24 42 10
11 34 02 20 43
44 12 30 03 21
22 40 13 31 04
Что полностью соответствует матрице индексов Вашего преобразования "строки диагонали".
Как видим, действительно, комбинация двух преобразований.
И это пример для квадрата 5-го порядка, то есть порядок является простым числом.
Мало интересно.
Для квадрата 9-го порядка
whitefox не давал мне ответ на этот вопрос.
А вы дадите?

Думаю, что одним преобразованием Q не справиться с моим примером для квадрата 9-го порядка. Нужно опять делать какую-то комбинацию преобразований. Какую?
У меня же не комбинация преобразований, а одно матричное преобразование.
*Ушёл

* И кто же мне теперь даст ответ
 -- Ср авг 21, 2013 10:03:12 --svb
-- Ср авг 21, 2013 10:03:12 --svb, ау!
Если преобразование в вашей статье, которое я здесь показала, имеет отношение к Теореме 3.3 Россера, тогда почему оно у вас работает только для нечётных n, а у Россера написано, что оно работает для всех n>=4?
-- Ср авг 21, 2013 10:36:17 --Вот система из 16 уравнений. Она состоит из 30ти известных (а) и 19ти неизвестных (х) и магической суммы S:
Уравнений действительно будет 16: сумма элементов в 7 строках, в 7 столбцах и в двух главных диагоналях.
Только что значит "30ти известных (а) и 19-ти неизвестных (х)"

Все элементы квадрата есть неизвестные величины в общей формуле квадрата (их ровно 49 в квадрате 7-го порядка); только одни из них свободные, а другие зависимые.
Вы уже точно знаете, что свободных переменных будет 30? Это вы свободные переменные называете известными?
В показанной мной выше формуле 34 переменных свободные и 15 - зависимые. Но я не знаю, правильно ли это. Может быть, свободных переменных будет меньше, если решить систему уравнений.