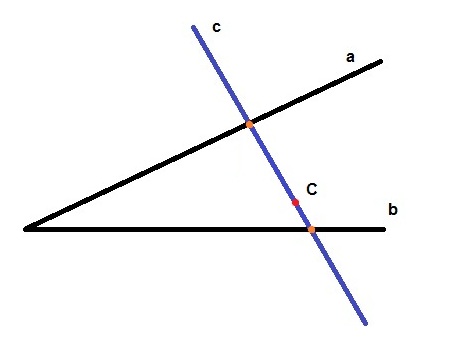
Размышляя над алгоритмом поиска прямого пути в графах, наткнулся на следующую подзадачу:
На плоскости есть две прямые
a,
b и точка
C. Через эту точку проходит третья прямая
c и пересекает первые две. Таким образом получаем две точки пересечения. Вычисляем расстояние между ними. Вращая прямую
с вокруг точки, получаем различные расстояния. Короче говоря, надо найти такой угол прямой
с, чтобы расстояние было наименьшим.
Вот картинка:
Я пытался решить аналитически. Посчитал, что точка пересечения первых двух прямых лежит в начале координат, затем вывел функцию расстояния от угла наклона прямой
с. Взял производную, но она получилась громоздкая, поэтому я оставил это дело. Численно задача довольно быстро решается, но хотелось бы все же узнать, можно ли решить аналитически.