Рассмотрим уравнение (11).
Уравнение (11) имеет решение (тема: уравнение (11) не имеет решения в целых числах):
![$y=l+(l/2)^{1/3} \cdot (\sqrt[3]{c+h}+\sqrt[3]{c-h}), \qquad l \geq 1\qquad$ $y=l+(l/2)^{1/3} \cdot (\sqrt[3]{c+h}+\sqrt[3]{c-h}), \qquad l \geq 1\qquad$](https://dxdy-03.korotkov.co.uk/f/e/d/f/edfb1a07ad4817bdf7cdd32d0bb0103282.png)
(1)

(2)
При условии

, решение (1) есть иррациональное число:
![$y=1+\sqrt[3]{2}+\sqrt[3]{4}$ $y=1+\sqrt[3]{2}+\sqrt[3]{4}$](https://dxdy-01.korotkov.co.uk/f/c/a/c/cac09ddaa6d02307f0eb4589f65b2e8182.png)
.
Рассмотрим (1) при условии

.
1.

.
![$y=2n+1+\sqrt[3]{c_{1}+(2n+1)h_{1}}+\sqrt[3]{c_{1}-(2n+1)h_{1}} \qquad$ $y=2n+1+\sqrt[3]{c_{1}+(2n+1)h_{1}}+\sqrt[3]{c_{1}-(2n+1)h_{1}} \qquad$](https://dxdy-04.korotkov.co.uk/f/7/8/c/78cb2b156168b9cde96c06c97c33ecee82.png)
(3)

(4)
2.

.
![$y=2n+\sqrt[3]{c_{2}+nh_{2}}+\sqrt[3]{c_{2}-nh_{2}} \qquad$ $y=2n+\sqrt[3]{c_{2}+nh_{2}}+\sqrt[3]{c_{2}-nh_{2}} \qquad$](https://dxdy-03.korotkov.co.uk/f/2/e/d/2ed31e53a4be3f4d6c3835b9d7135d7382.png)
(5)

(6)
Рассмотрим уравнение:

(7)
Найдем целые значения числа

, при которых

целое число.
Уравнение (7) имеет одно положительное решение:

(8)
Рассмотрим равенство:

(9)

- целое число. Если

целое число, то

целые числа одной чётности. В этом случае, уравнение (9) можно представить в виде:

(10)
Для целых чисел

, равенство (10) невыполнимо. Итак, для целого числа

не является целым числом. Согласно (4),

иррациональное число.
Рассмотрим уравнение:

(11)
Найдем целые значения числа

, при которых

целое число.
Уравнение (11) имеет одно положительное решение:

(12)
Рассмотрим равенство:

(13)

- целое число. Если

целое число, то

целые числа одной чётности. В этом случае, уравнение (13) можно представить в виде:

(14)
Согласно(9), для целых чисел

, равенство (14) невыполнимо. Итак, для целого числа

не является целым числом. Согласно (6),

иррациональное число.
Введем обозначения:

(15)
Для целого числа
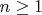
,

не являются полными квадратами целых чисел. Такие числа можно единственным образом представить в виде:

(16)

- целые числа,

- простые числа. В общем случае,

это произведения простых чисел не равных друг другу:



простые числа,

.
С учётом (15) и (16),

равны:

(17)
Согласно (17),

иррациональные числа, по определению. С учётом (17), решения (3) и (5) равны:
![$y=2n+1+\sqrt[3]{u_1}+\sqrt[3]{v_1}, \qquad u_1>v_1>0 \qquad$ $y=2n+1+\sqrt[3]{u_1}+\sqrt[3]{v_1}, \qquad u_1>v_1>0 \qquad$](https://dxdy-03.korotkov.co.uk/f/6/4/f/64f15fa5b4273e725b7ec28e07dc5a5982.png)
(18)

(19)
![$y=2n+\sqrt[3]{u_2}+\sqrt[3]{v_2}, \qquad u_2>v_2>0 \qquad$ $y=2n+\sqrt[3]{u_2}+\sqrt[3]{v_2}, \qquad u_2>v_2>0 \qquad$](https://dxdy-01.korotkov.co.uk/f/0/f/2/0f215424896f7b08683e35eacf42102382.png)
(20)

(21)
Согласно (19) и (21),

есть иррациональные алгебраические выражения, по определению. В этом случае,
![$(\sqrt[3]{u_i}, \sqrt[3]{v_i})$ $(\sqrt[3]{u_i}, \sqrt[3]{v_i})$](https://dxdy-01.korotkov.co.uk/f/0/5/9/05984cc28ca3714344a83ccf000f489082.png)
это радикалы из иррациональных выражений. Следовательно, эти радикалы могут быть только иррациональными числами. Итак, правые части решений (18) и (20) являются иррациональными алгебраическими выражениями, по определению.
И последнее, если допустить, что правые части (18) и (20) есть целые числа, то, следовательно, теорема Ферма неверна.
-- 12.12.2012, 11:07 --Someone!
Спасибо!
Книгу я уже скачал.
Итак, имеем формулы. Что дальше с ними делать. Фактически исходное уравнение при данных условиях представлено в ином виде и более сложном.