1.Сильная проблема Гольдбаха. Каждое чётное число, большее 2, можно представить в виде суммы двух простых чисел.
2.Постулат Бертрана, теорема Бертрана — Чебышева или теорема Чебышева гласит, что
Для любого натурального

найдётся простое число p в интервале
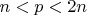
.
-- 08.06.2012, 13:37 --А)Постулат Неймета гласит(усиленный Постулат Бертрана), что
Для любого простого

следующее простое число

будет находится в интервале

Возьмем последовательность чисел

, причем
![$a_{k}=(1+2+3+4+...+P_{k})/2+P_{k}$
или $a_{k} +1$ ,eсли $a_{k}$- парное)
B)Tеорема. Если число [math]$2*P_{k}-2$ $a_{k}=(1+2+3+4+...+P_{k})/2+P_{k}$
или $a_{k} +1$ ,eсли $a_{k}$- парное)
B)Tеорема. Если число [math]$2*P_{k}-2$](https://dxdy-01.korotkov.co.uk/f/0/4/3/04347cc3230da4d059c10a3755a449c282.png)
покрыто из интервала

, тогда и только тогда когда

- близнецы.
Док-во:

и
из п.1(Сильная проблема Гольдбаха) следует,

- простые (близнецы)