Я хочу доказать следующую
вспомогательную лемму:
Пусть

, тогда числа
![$[a], [2a], [3a], \dots, [Na]$ $[a], [2a], [3a], \dots, [Na]$](https://dxdy-04.korotkov.co.uk/f/b/d/7/bd771bca47335cc2c582c09892e974be82.png)
различны между собой.
Доказательство:Верны следующие неравенства:

, где
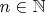
. Так как целая часть - функция неубывающая, то:
![$[(n+1)a]\leqslant [na]$ $[(n+1)a]\leqslant [na]$](https://dxdy-02.korotkov.co.uk/f/1/e/2/1e244f3ae8d9c4f351d6487454bbe50582.png)
Пусть все-таки они совпадают, т.е.
![$[(n+1)a]=[na]=k$ $[(n+1)a]=[na]=k$](https://dxdy-02.korotkov.co.uk/f/9/4/4/9446b1ba8736e6d5965daccf5a83f69c82.png)
.
Так как

, то
![$[na]<-1$ $[na]<-1$](https://dxdy-04.korotkov.co.uk/f/3/b/3/3b311d6fb4007687fae2cb3ec2bdcc8d82.png)
, т.е.

Получаем систему неравенств:

Это равносильно следующему:

Покажем, что имеют места неравенства:

Нам достаточно доказать неравенство

, так как остальные очевидны.
Умножаем обе части на

и получаем:




А последнее неравенство верно так как

, то

.
Из последнего получаем, что
![$[(n+1)a]<-(n+1)$ $[(n+1)a]<-(n+1)$](https://dxdy-01.korotkov.co.uk/f/c/a/f/caf59aabffc04229752f9376c9c9671d82.png)
, т.е.

или

.
Получаем, что число

попадает одновременно в две непересекающиеся множества, а этого быть не может. Значит,
![$[(n+1)a]<[na]$ $[(n+1)a]<[na]$](https://dxdy-03.korotkov.co.uk/f/e/5/1/e519ccddfbc3e415b84df70f47e70f5c82.png)
Скажите пожалуйста то, что я написал смахивает ли это на доказательство?