_hum_, возражений нет, но можете [при желании] изложить и "классическую" трактовку.
По Ширяеву:
рассмотрим случайные величины (с.в.)
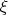
и

. Предположим, что наблюдению подлежит лишь с.в.

. Если величины не являются независимыми, то можно ожидать, что знание значений

позволит вынести некоторые суждения и о значении ненаблюдаемой величины

. Всякую функцию

будем называть
оценкой для

. Будем говорить, что оценка
 оптимальна в среднеквадратичном смысле
оптимальна в среднеквадратичном смысле, если

Допустим, что мы интересуемся оптимальными только в классе линейных оценок, то есть оценок вида

, где

-- вещественные параметры. В этом случае легко решить задачу поиска минимума по двум параметрам и прийти к выражению для оптимальной в среднеквадратичном смысле линейной оценки:

с величиной среднеквадратичной ошибки:

где

- ковариация с.в.,

- коэффициент корреляции.
Отсюда видно, что ковариация определяет коэффицент линейной части оценки - если она положительна, то зависимость прямая (чем больше значения

, тем они больше и у

), если нет - обратная. Корреляция определяет величину ошибки оценивания - чем она ближе к единице, тем ошибка меньше.
Как-то так...
А, ну да, обычно подчеркивается, что ковариация/корреляция служит мерой именно
линейной зависимости между с.в. и ее равенство нулю еще не говорит о том, что зависимости нет, ибо она может быть нелинейная.