Мне хотелось ещё пояснить и уточнить своё синее заявление:
Ни клотоида, ни кубическая парабола, ни какая-либо другая каноническая кривая эту задачу в общем виде не решают.
Чтобы построить кривую, идущую из точки

в точку

с заданными наклонами касательных и кривизнами в граничных точках, мы должны удовлетворить 5 равенств относительно параметров, не зависящих от поворотов и переносов: длины хорды

, наклонов касательных

, измеренных относительно хорды
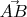
, и кривизн

(случай

следовало бы рассмотреть отдельно).
Чтобы решать задачу в переменных, также не зависящих от движений, будем исходить из натурального уравнения

некоторой кривой. Здесь

--- кривизна и длина дуги,

--- параметры, модифицирующие форму кривой. Обычно один из них,

, отвечает за размер (подобие), остальные, безразмерные, --- какие-то характерные углы, отношения, итп. У коники это фокальный параметр и эксцентриситет; у логарифмической спирали параметра

нет, только

(постоянный угол между кривой и полярным лучом). Стало быть, для решения задачи нам надо брать кривую, имеющую хотя бы 3 параметра формы. Вместе с началом

и концом

дуги это даст пять свободных параметров для составления пяти уравнений относительно вышеуказанных пяти неизвестных.
Спираль Корню и квадратичная парабола имеют только по одному параметру формы

(у первой это расстояние между асимптотическими точками, у второй --- фокальный параметр). С

мы можем рассчитывать реализовать только 3 заданные величины, например,

.
У кубической параболы два параметра формы:

(пропущенные коэффициенты обнуляются соответствующими параллельными переносами). В том или ином виде они перейдут в два параметра

натурального уравнения. С этим можно надеяться удовлетворить, кроме

, одну из кривизн. В этом смысле кубическая парабола эквивалентна конике (фокальный параметр + эксцентриситет), с той лишь разницей, что заполучить точку перегиба с коникой не удастся. Но можно, при желании, заполучить гиперболу с разрывом внутри.
Так что начинать надо с параболы

(не видел, чтобы кто-то этим занимался; наверное, попробовали и бросили). Глянув по диагонали атлас плоских кривых, зацепил только кривую Персея, у которой, похоже, имеется необходимая прорва параметров формы.
Но стоит проинвертировать хотя бы квадратичную параболу, и мы получим набор

: два последних параметра появятся за счёт варьирования центра инверсии; радиус инверсии повлияет лишь на масштаб, дополнительной степени свободы не даст. А ежели заметить, что

--- инверсный инвариант (знак только меняет), и угол пересечения граничных кругов кривизны тоже, то необходимую дугу параболы можно подобрать заранее. Её и инвертировать. Лучше Мёбиусом, по трём точкам, оставляя граничные точки неподвижными, и двигая, например, бесконечно удалённую точку (те же две дополнительные степени свободы).
Кривая, замечу, получится рациональной.
Сумеем параболу (или другую конику) без вершины подобрать, --- будет нам у полученой кривой ещё и вожделенная монотонность кривизны.