Есть такая задача.
Естественная система криволинейных координат, связанная с плоской кривой

, заданной своим радиусом кривизны

как функция длины дуги

. Положение точки

на плоскости определяется длиной нормали

к контуру

, проходящей через точку

и длиной дуги

, отсчитываемой от некоторой точки

контура до основания нормали

. Угол

-- прямой. Найти коэффициенты Ламе
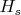
и

.
Очевидно, по условию, такая система координат -- ортогональная. Коэффициенты Ламе определяются отсюда:
![$\[d{S^2} = H_s^2d{s^2} + H_n^2d{n^2}\]$ $\[d{S^2} = H_s^2d{s^2} + H_n^2d{n^2}\]$](https://dxdy-03.korotkov.co.uk/f/e/f/4/ef4c4a8d80127f6d94ea2b4388cb1f9782.png)
. А если задать прямоугольную систему координат и как-то получить связь

и

, то эти коэффициенты можно получить из формул:
![$\[{H_s} = \left| {\frac{{\partial {\text{r}}}}
{{\partial s}}} \right|; \, {H_n} = \left| {\frac{{\partial {\text{r}}}}
{{\partial n}}} \right|\]
$ $\[{H_s} = \left| {\frac{{\partial {\text{r}}}}
{{\partial s}}} \right|; \, {H_n} = \left| {\frac{{\partial {\text{r}}}}
{{\partial n}}} \right|\]
$](https://dxdy-02.korotkov.co.uk/f/1/f/c/1fc64b848c3fc89537f2bb1f3d8bfdc782.png)
Достаточно ясно, что

. Вопрос в
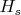
. Ведь при фиксировании

и изменении

центр кривизны как-то смещается, и не могу сообразить, как в этом случае находить

.
 -- Пт сен 17, 2010 21:48:09 --
-- Пт сен 17, 2010 21:48:09 --Сообразил такую формулу:
![$\[dS = ds\left| {\frac{{d{\text{r}}}}
{{ds}} \pm n\frac{{d{\text{n}}}}
{{ds}}} \right|\]
$ $\[dS = ds\left| {\frac{{d{\text{r}}}}
{{ds}} \pm n\frac{{d{\text{n}}}}
{{ds}}} \right|\]
$](https://dxdy-04.korotkov.co.uk/f/f/6/5/f65a59790a3b3a2531058dce9a53834582.png)
. Здесь плюс или минус зависит от расположения точки относительно кривой,
![$\[{\text{n}}\]$ $\[{\text{n}}\]$](https://dxdy-01.korotkov.co.uk/f/8/7/2/872640215d631b980345dea8293e598582.png)
-- единичный вектор главной нормали. Можно ли как-то это все закрутить с радиусом кривизны?