2
AnonimiusЦитата:
Значит и при отклонение 0 они ПЕРЕСЕКАЮТСЯ!
Если они пересекаются, то они уже не являются параллельными, по-определению.
На самом деле unsigned 0 - очень абстракное понятие, потому что на самом деле 0 есть ноль для соразмерных между собой чисел тех, что больших нуля (по модулю бесконечно больших, чем 0).... unsigned 0, по сути - бесконечное множество континиумов бесконечно малых: каждый континиум определяет множество соразмерных бесконечномалых: т. е. пусть c=0+ - некоторое положительное бесконечномалое тогда соответствующий ему континиум {

}

, где

, потому что если определить 1 = c, полученный континиум будет совпадать с множество действительных чисел. Все эти соразмерные между собой числа - бесконечно малые и для настоящей единицы будут выглядить как 0. Более того, существут бесконечная последовательность континумов, любой элемент из каждого последующего представителя которой, будет бесконечно больше, любого представителя из приведущего, т. е. выглядить в его измерении, как

, но для действительной единицы все они 0+. Все эти рассуждения можно рекурсивно повторить и для 1 = c:

по
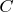
и т. д. С бесконечностью можно проделать примерно все тоже самое..