Теория групп (строговозрастающие непрерывные функции)

[Taras]

То.

[G_Ray]

Всех с наступившим новым годом! Спасибо за помощь оказанную в прошлом году

Продолжим с теорией групп:


Задание:
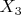
В свободной абелевой группе $X_3$ со свободными порождающими $x_1$, $x_2$,$x_3$ задана подгруппа $Y$ с порождающими:
$ \left\{ \begin{array}{l} y_1= 4x_1+12x_2+20x_3 \\ y_2= 24x_1+8x_2-8x_3 \\ y_3=24x_1+24x_2+24x_3 \end{array} \right. $
а) Найти разложение фактор-группы в прямую сумму циклических подгрупп
б) Указать силовские подгруппы в $X_3/Y$
в) Найти порядок элемента $x_1+x_2+x_3 + Y$ в $X_3/Y$

Решение:
а) Значит методом эквивалентных преобразоаний (или как их там (можно умножать только на (-1) и складывать строки и столбцы) я матрицу:
$ \left( \begin{array}{ccc} 4 & 12 & 20 \\ 24 & 8 & -8 \\ 24 & 24 &24 \end{array} \right)$
привел к такому виду:
$ \left( \begin{array}{ccc} 16 & 0 & 0 \\ 0 & 16 & 0 \\ 0 & 0 & 4 \end{array} \right)$
Следовательно
$<X_3>/<Y>$ = $Z_{16}+Z_{16}+Z_4$ Правильно?
б, в)Вот тут уже проблемы.
Подскажите пожалуйста.

[G_Ray]

И ещё хитрый такой вопрос. Бывают ли "фактор-поля" или что-то типо того?

[AV_77]

G_Ray писал(а):

И ещё хитрый такой вопрос. Бывают ли "фактор-поля" или что-то типо того?

Факторполей не бывает, а "что-то типа того" вполне - факторкольца, факторалгебры, etc.

[Профессор Снэйп]

G_Ray писал(а):

И ещё хитрый такой вопрос. Бывают ли "фактор-поля" или что-то типо того?

Для колец бывают поля частных. Не знаю, "типо того" это или не "типо".

[mkot]

G_Ray писал(а):

И ещё хитрый такой вопрос. Бывают ли "фактор-поля" или что-то типо того?

Что не бывает уже было сказано.
Постараюсь объяснить почему.
Факторкольца строятся с помощью идеалов, факторгруппы строятся с помощью нормальных подгупп. Идеалы и нормальные подгруппы имеют общее происхождение -- они являются ядрами гомомфизмов. Но для полей не имеет смысла говорить о гомоморфизмах, так как если предположить, что существует гомоморфизм $f$ поля $K$ в поле $K'$ такой, что $\mathrm{ker}\, f \neq 0$, то $\mathrm{ker}\, f = K$.

[Someone]

Профессор Снэйп в сообщении #174124 писал(а):

Для колец бывают поля частных. Не знаю, "типо того" это или не "типо".

Нет, это совсем другое.

[vlad239]

G_Ray писал(а):

б) Указать силовские подгруппы в $X_3/Y$

Следовательно
$<X_3>/<Y>$ = $Z_{16}+Z_{16}+Z_4$ Правильно?
б, в)Вот тут уже проблемы.
Подскажите пожалуйста.

Если нигде не обсчитались, то пункт б очевиден. Чему равен порядок этой группы? Чему равен тогда порядок ее силовской 2-подгруппы (других нет, понятно)? Как Вы думаете, что ж это за подгруппа такая?

Влад.

[Klarissa]

Задача:
Перечислить возможно большее число неизоморфных групп порядка 17 и 12. Доказать, что перечисленные группы попарно неизоморфны.

Как эти группы вообще искать?

[vlad239]

Klarissa писал(а):

Задача:
Перечислить возможно большее число неизоморфных групп порядка 17 и 12. Доказать, что перечисленные группы попарно неизоморфны.

Как эти группы вообще искать?

17 - простое число.

12 - вспомните, какие вообще группы маленьких порядков Вы знаете и возьмите у некоторых из них прямые произведения.

(насколько я помню, групп порядка 12 -- 5 штук, при этом 4 можно построить легко, а вот как легко догадаться до пятой и тем более доказать, что нет других (без муторного перебора) - я не знаю. К счастью, Вам не надо придумывать ВСЕ.)

[Klarissa]

vlad239 писал(а):

Задача:
12 - вспомните, какие вообще группы маленьких порядков Вы знаете и возьмите у некоторых из них прямые произведения.

Можете объяснить поподробнее?
Теория групп - слишком абстрактная математика, никак не могу разобраться:-(

[vlad239]

Klarissa писал(а):

Можете объяснить поподробнее?
Теория групп - слишком абстрактная математика, никак не могу разобраться:-(

Могу но не стану. Работайте сами. Какие Вы вообще знаете конечные группы? Что такое прямое произведение?

Влад.

[Palza]

Скажите, пожалуйста, что понимается под фразой "подгруппа стабильности"

[Palza]

что значит "модуль группы"?

[Brukvalub]

Palza в сообщении #178701 писал(а):

Скажите, пожалуйста, что понимается под фразой "подгруппа стабильности"

Palza в сообщении #178840 писал(а):

что значит "модуль группы"?

Знаете, почему никто не отвечает? Потому, что без контекста нет однозначности в толковании этих терминов. Например, "подгруппа стабильности", возможно, означает "подгруппа тех элементов группы преобразований, которые оставляют неподвижной данную точку". А может означать и нечто другое, но гадать - лень.
Расширьте цитаты, дописав окружающие их фразы.