Задача про полоски с дырками

[mihaild]

anahronizm в сообщении #1717915 писал(а):

Да что с меня взять? Я ж не математик, поэтому мне можно

Нет, нельзя. Ну в смысле расстреливать Вас как ТС в ПРР(М) за ошибки никто не будет, но это всё еще остается ошибкой.

(Оффтоп)

Вообще, не очень понятно, чего Вы ожидаете, повторяя, что не математик. Я тоже не математик, ну и что?

anahronizm в сообщении #1717915 писал(а):

Думаю, waxtep и wrest даже смогут подтвердить верность таких утверждений

Думаю не могут. По крайней мере пока что сообщений, что задача решена, от них не было. И вполне может оказаться, что задача вообще далеко за пределами возможностей современной математики.

anahronizm в сообщении #1717915 писал(а):

групп из двух, подряд идущих не проколотых клеток на периоде (если рассматривать бесконечную полоску) будет всегда нечётное количество

А это, если я не обсчитался, неправда уже для первой вилки, если оба прохода ей начинать с первой клетки.

[anahronizm]

mihaild в сообщении #1717919 писал(а):

если я не обсчитался

Думаю, Вы обсчитались. А может я не точно описал ситуацию (такое может быть).
А про не математика, так это правда же.
К Вам и другим собеседникам с моим уважением - это тоже правда.

[wrest]

mihaild в сообщении #1717919 писал(а):

Думаю не могут.

Я - нет, не могу.

[waxtep]

mihaild в сообщении #1717919 писал(а):

А это, если я не обсчитался, неправда уже для первой вилки, если оба прохода ей начинать с первой клетки.

anahronizm в сообщении #1717922 писал(а):

Думаю, Вы обсчитались. А может я не точно описал ситуацию (такое может быть).

А это же зависит от того, с какого места начинать отсчет периода. На том же примере двух проходов одной вилки, тыкаем левым зубцом в обоих проходах в клетку номер 1. Берем период с 1 до 35, получаем три двухклеточных дырки: (4,5), (19,20), (34,35). Теперь берем период с -1 до 34 и имеем только две таких, (4,5), (19,20) (но если мысленно замкнуть период в цикл, будет и третья (34,-1)). anahronizm, а почему Вы такой упор на двухклеточные дырки делаете, думаете, это чем-то поможет решению задачи?

Задача, кстати, может быть, на 7-ой странице топика пора ее аккуратно сформулировать, а то сейчас элементы постановки разбросаны по топику. Я попробую для пользы дела, но тоже не математик, извините, если что. Итак: для данного $k\in\mathbb{N}$ найти максимальное $M=M(k)\in\mathbb{N}$, такое, что $\forall{m}\in\mathbb{N},1\leqslant m\leqslant M\,\exists i\in\mathbb{N},1\leqslant i\leqslant k:$

$$m\equiv (b_i^--i)\bmod(6i-1)\vee m\equiv (b_i^-+i)\bmod(6i-1)\vee \\ m\equiv (b_i^+-i)\bmod(6i+1)\vee m\equiv (b_i^++i)\bmod(6i+1)$$

где $b_i^-,b_i^+\in\mathbb{Z}$ - $2k$ остатков по модулям $6i\pm1$, оптимальный подбор которых и дает максимальное $M$ для данного $k$.
Можно варьировать вопрос, не "найти максимальное $M(k)$", а "доказать или опровергнуть $\exists k_0: \forall k\geqslant k_0\, M(k)\geqslant 8k+4$" (исходная формулировка задачи) или "получить хорошую оценку снизу и сверху для $M(k)$", "доказать или опровергнуть конечность $M(k)$ для всех $k$" и т.п.
Можно варьировать количество прогрессий и их шаг; mihaild приводил ссылку на статью, из которой следует конечность $M(k)$ для всех $k$ для однозубой вилки (условие вида $m\equiv b_i^-\bmod(6i-1)\vee m\equiv b_i^+\bmod(6i+1)$).

В целом по задаче придерживаюсь такого же мнения:

anahronizm в сообщении #1717787 писал(а):

такие данные дают только направления для исследований ?

mihaild в сообщении #1717919 писал(а):

И вполне может оказаться, что задача вообще далеко за пределами возможностей современной математики.

Что касается счетного прогресса, он у меня пока слабый. Поверив в $M(5)=71,M(6)=126$ (это не доказанный факт, возможно, соответствующие $M(k)$ больше), пытаюсь штурмовать $M(7)$. Нашел какими-то шаманскими методами две стратегии с $M=150$, но это маловато, жду $M(7)>215$. Подсчет $M(7)$ по программе, опирающуюся на эвристику, использованную для расчета $k=5,6$, займет около 32 месяцев на моей технике; расчет по полному периоду - 8 с лишним тысячелетий, долгонько. Хочется найти какую-то еще эвристику. То что я делаю, скорее, не математика, а поиск закономерностей, в том числе какими-то сомнительными способами. Ну, поиск он на то и поиск

[anahronizm]

waxtep в сообщении #1718022 писал(а):

с какого места начинать отсчет периода

Вы правы, именно поэтому я указывал, что "Для уточнения: за начало периода нужно принять ту клетку(точку), куда попадёт левый зубец каждой вилки."
Если мы возьмём Ваш пример, когда рассматриваем интервал от -1 до 34, то -1 разрывает группу из двух, подряд не проколотых клеток и таких групп останется две.

waxtep в сообщении #1718022 писал(а):

anahronizm, а почему Вы такой упор на двухклеточные дырки делаете, думаете, это чем-то поможет решению задачи?

Думаю, да. Сам-то я решать не умею, тут нужны знатоки Китайской теоремы, но некоторые предположения я мог бы сделать.
Возможно, для первых двух вилок с их двумя проходами, на полном периоде, который будет равен 5005, количество групп из двух, подряд не проколотых клеток, будет равно 189, но могу ошибаться.

waxtep в сообщении #1718022 писал(а):

Задача, кстати, может быть, на 7-ой странице топика пора ее аккуратно сформулировать

Было бы очень здорово! Я уж думал над этим и просил собеседников. Сам я сформулировал, как смог - получилось, видимо, совсем криво.
Если задача показалась интересной, то стило бы её правильно озвучить, возможно, с другими, более значимыми, вопросами.
И вот ещё мысль: частным случаем данной задачи является вариант, когда левый зуб вилки совпадает с правым зубом и проход каждой вилки осуществляется 1 раз.
А при общем случае, можно было бы задать и размер дырки и количество проходов каждой вилкой.

-- 11.02.2026, 10:04 --

waxtep в сообщении #1718022 писал(а):

Можно варьировать количество прогрессий и их шаг; mihaild приводил ссылку на статью, из которой следует конечность $M(k)$ для всех $k$ для однозубой вилки (условие вида $m\equiv b_i^-\bmod(6i-1)\vee m\equiv b_i^+\bmod(6i+1)$).

Как жаль, что я в этом совсем ничего не понимаю !!!

-- 11.02.2026, 10:26 --

Кстати, по поводу симметрии распределения.
Начало симметрии нужно рассматривать как середину дырки первого удара первой вилки (при условии, что все последующие вилки при каждом проходе левым зубцом попадут в ту клетку(точку), куда ударил левый зубец первой вилки).
Как-то так. Нужно бы этот вопрос продумать.

[waxtep]

anahronizm в сообщении #1718036 писал(а):

Сам я сформулировал, как смог - получилось, видимо, совсем криво.
Если задача показалась интересной, то стило бы её правильно озвучить, возможно, с другими, более значимыми, вопросами.
И вот ещё мысль: частным случаем данной задачи является вариант, когда левый зуб вилки совпадает с правым зубом и проход каждой вилки осуществляется 1 раз.
А при общем случае, можно было бы задать и размер дырки и количество проходов каждой вилкой.

Да, слушайте, несколько человек Вас поняло и приняло участие в обсуждении задачи, - кажется, не о чем переживать. Я попытался чуть строже сформулировать задачу, чтобы дать потенциально заинтересованным участникам понять предмет обсуждения, без погружения в интимную жизнь вилок, полосок и проколов на семи страницах
А дальнейшие трудности в прогрессе решения задачи, по всей видимости, уже связаны с высокой сложностью задачи по существу, а не с непонятностью формулировок. Вот, про однозубые вилки (грубо говоря) есть упоминавшаяся статья, написанная математиками-специалистами в теории чисел. Из нее, в частности, следует, что проколы однозубыми вилками с периодами, не кратными ни $2$, ни $3$, никогда не покроют бесконечную полоску сплошняком. Можно ли их доказательство адаптировать для двузубых вилок? Я не пробовал, не знаю.

anahronizm в сообщении #1718036 писал(а):

Как жаль, что я в этом совсем ничего не понимаю !!!

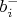
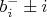
Это просто способ изложения, он, в общем, не приближает и не удаляет решение задачи. $b_i^-$ - это положение серединки $i$-той вилки в первом проходе, для какого-то из уколов. Ее зубцы прокалывают клетки $b_i^-\pm i$ в этом уколе. Ну, а все уколы $i$-той вилки в первом проходе повторяются с периодом $6i-1$, что можно обозначить как $\{b_i^-\pm i+n\cdot(6i-1),\forall n\in\mathbb{Z}\}$. 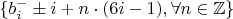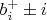$b_i^+\pm i$ - все то же самое для второго прохода $i$-той вилки с периодом $6i+1$.

anahronizm в сообщении #1718036 писал(а):

Начало симметрии нужно рассматривать как середину дырки первого удара первой вилки

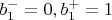
Да, тоже счел удобным смотреть на положение середки каждой вилки в каждом проходе, и всегда беру $b_1^-=0,b_1^+=1$, а остальные вилки уже относительно этих зафиксированных точек позиционирую. Это, конечно, всегда допустимо, потому что всю серию любых проколов целиком всегда можно сместить на любое количество клеток влево или вправо (задача "имеет трансляционную симметрию").
Что касается каких-либо закономерностей... вот, для примера, положение серединок вилок для случая пяти вилок, когда удается проколоть $71$ клетку подряд (мне это кажется максимально возможным, но не доказал):

[ 1   0]
[ 2   1]
[ 3   5]
[ 4  -5]
[ 5  -5]
[ 6  -8]
[ 7   9]
[ 8  -9]
[ 9 -12]
[10  12]

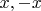
Первая колонка - номер "вилко-прохода", 1 - первый проход первой вилки, 2 - второй ее же, 3 - первый проход второй вилки и т.п. Аж три вхождения $x,-x$ для соседних вилко-проходов. Случайность или нет? (я лично думаю, что случайность; другие предположительно оптимальные стратегии так не выглядят; но, кто знает)

anahronizm в сообщении #1718036 писал(а):

(при условии, что все последующие вилки при каждом проходе левым зубцом попадут в ту клетку(точку), куда ударил левый зубец первой вилки)

Эту часть, честно говоря, не понял, можете пояснить? На общем периоде встретится и такое, конечно (тут надо аккуратно уточнить утверждение при наличии не взаимнопростых периодов), но сплошняком покрытая проколами полоска может оказаться очень-очень далеко от этой конфигурации. И при машинном счете (меня все в эту сторону клонит ) до нее за разумное время, возможно, не удастся дойти. Но можно проверить для небольших $k$, посмотрю попозже

-- 11.02.2026, 22:46 --

waxtep в сообщении #1718091 писал(а):

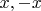
Аж три вхождения $x,-x$ для соседних вилко-проходов

Это, собственно, значит, что одной и той же вилкой оптимально иногда кольнуть симметрично в первом и втором проходе относительно середины укола первой вилкой в первом проходе. Ну... бог знает

-- 11.02.2026, 23:05 --

Тут, знаете, тоже надо аккуратно выражаться, конечно. То же самое можно записать и в полностью симметричном виде:

[ 1 0]
[ 2 1]
[ 3 5]
[ 4 -5]
! [ 5 46]
! [ 6 -46]
[ 7 9]
[ 8 -9]
[ 9 -12]
[10 12]

Просто всюду, кроме вилко-проходов 5, 6 числа (координаты симметрично расположенных серединок вилок) "несколько меньше". Интересно, может быть из этого что-то можно вытащить

-- 11.02.2026, 23:27 --

Иными словами, можно проверить такую эвристику: оптимальную стратегию, максимизирующую $M(k)$ следует искать в виде

$$b_i^-=-b_i^+,|b_i^-|<6\cdot t\cdot i$$

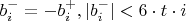
где $t$ - "достаточно малое число", двойка там, тройка, ну, может, десятка. При этом покрытая полоска будет включать промежуток $[-1;2]$. Я это попробую чуть позже, пожалуй

[waxtep]

waxtep в сообщении #1718091 писал(а):

Иными словами, можно проверить такую эвристику: оптимальную стратегию, максимизирующую $M(k)$ следует искать в виде

$$b_i^-=-b_i^+,|b_i^-|<6\cdot t\cdot i$$

где $t$ - "достаточно малое число", двойка там, тройка, ну, может, десятка

Нет, не похоже, что это всегда работает. По крайней мере, для шести вилок есть пять с виду различных стратегий, позволяющих покрыть (недоказанно) максимальные $126$ клеток. Если записать для них значения $|b_i^-|=|b_i^+|$ для всех вилок, начиная со второй, то выйдет

$$\begin{array} |\\ (18,138,211,331,509)\\ (27,154,54,417,544)\\ (36,153,256,266,579)\\ (47,63,199,416,536)\\ (56,79,66,332,571)\end{array}$$

и все трехзначные числа выглядят великовато. Может быть, есть "примерно симметричные" варианты "недалеко от эпицентра", но это хорошо бы сперва формализовать, и затем проверить

[anahronizm]

waxtep в сообщении #1718091 писал(а):

(при условии, что все последующие вилки при каждом проходе левым зубцом попадут в ту клетку(точку), куда ударил левый зубец первой вилки) Эту часть, честно говоря, не понял, можете пояснить?

Это пояснение только для определения, где именно находится та дырка, середина которой будет являться началом симметрии. Это ситуация, когда все вилки при всех проходах начинают бить с одной точки (вернее, их левый зубец).
На бесконечной полоске такое место (обязательно) будет появляться один раз за период. Т.е. всегда будет ситуация на бесконечной полоске, что при любых количествах вилок (можно ли тут применить понятие бесконечности?) все вилки ударят левым зубом в одну точку. А вот что будет происходить с правыми зубьями вилок на периоде - тоже интересно. И даже очень интересно, особенно в плане поиска оптимальной стратегии забития (но это только интуиция). Совершенно уверен, что можно вывести формулу максимально забитого участка - его длины и координаты. И если я прав в том, что такое разбиение обладает симметрией и содержит в своей середине группу максимального размера из непробитых клеток (таких групп на периоде нечётное количество при условиях исходной задачи), то максимально забитых участка на периоде будет, как минимум, два.
Наверное, это всё требует доказательств, хоть мне и кажется очевидным.
Сдаётся мне, вопрос максимального забития может быть интересен и в практическом плане. В том числе и вопрос отношения длины забитой полоски к количеству таких клеток в ней, которые были пробиты более одного раза - т.е. вопрос эффективности.

anahronizm в сообщении #1718036 писал(а):

Возможно, для первых двух вилок с их двумя проходами, на полном периоде, который будет равен 5005, количество групп из двух, подряд не проколотых клеток, будет равно 189, но могу ошибаться.

Вот не уверен, что прав в этом вопросе, может кто подскажет ?

[waxtep]

waxtep в сообщении #1718096 писал(а):

Может быть, есть "примерно симметричные" варианты "недалеко от эпицентра", но это хорошо бы сперва формализовать, и затем проверить

Ага. Ну, вот, для шести вилок, есть стратегия, удовлетворяющая такой эвристике (Э1):

$$|b_i^-+b_i^+|\leqslant1,|b_i^-|<18\cdot i$$

И такой тоже (Э2):

$$|b_i^-+b_i^+|\leqslant3,|b_i^-|<12\cdot i$$

Вот она, слева в непричесанном виде (показаны положения ближайших к эпицентру середок между проколами), а справа - в виде, удовлетворяющем Э1 или Э2:

raw           Э1          Э2
[ 1   0]   [ 1   0]    [ 1   0]
[ 2   1]   [ 2   1]    [ 2   1]
[ 3   5]   [ 3   27]   [ 3   16]
[ 4  -1]   [ 4  -27]   [ 4  -14]
[ 5   1]   [ 5   1]    [ 5   1]
[ 6  -2]   [ 6  -2]    [ 6  -2]
[ 7  -8]   [ 7  -54]   [ 7  -31]
[ 8   4]   [ 8   54]   [ 8   29]
[ 9  11]   [ 9  -18]   [ 9   11]
[10 -14]   [10   17]   [10  -14]
[11 -16]   [11  -86]   [11  -51]
[12  11]   [12   85]   [12   48]

Выглядит перспективно, можно попробовать побороться

[waxtep]

waxtep в сообщении #1718132 писал(а):

Выглядит перспективно, можно попробовать побороться

Не, это фигня. Стратегия Э1 требует расчета $60^{k-1}\cdot (k-1)!$ вариантов против $4^{k-1}\cdot (2k-2)!$ в имеющейся стратегии. Это лучше при $k\geqslant11$, но в обеих стратегиях уже при $k=11$ астрономическое число вариантов ($>2\cdot10^{24}$). Эх!

[waxtep]

waxtep в сообщении #1718141 писал(а):

астрономическое число вариантов ($>2\cdot10^{24}$)

Короче, перед всем этим астрономическим многобезобразием, я лично склонен пуститься во все тяжкие и попробовать жадные пошаговые стратегии. Например:
1. Делаем проколы первой вилкой, выбираем какой-то островок из четырех проколотых клеток подряд в качестве эпицентра;
2. Берем некоторое количество прогрессий (две-четыре), пытаемся пристроить слева-справа к эпицентру;
3. Перебираем все такие варианты, и для дальнейшего расчета оставляем только один, максимизирующий сумму квадратов длин островков из проколотых подряд клеток; ведь чтобы в конце была проколота полоска максимальной длины, на промежуточных шагах должно образоваться несколько "жирных" островков. Ну и просто сумму длин максимизировать бесполезно, нужен учет того, что одна полоска из четырех клеток подряд ценнее, чем четыре одноклеточных;
4. После выбора варианта, повторяем шаги 2-3 с оставшимися прогрессиями, и так до упора.

Возможно, какие-то еще усложнения понадобятся, поскольку в таком виде, наверное, предпочтение при самом первом выборе варианта будет отдаваться прогрессиям с наименьшим шагом, что, возможно, не всегда оптимально. Типа штрафного коэффициента в зависимости от шага прогрессии.

Цель упражнения - попытаться получить "хорошую" оценку снизу для максимального размера непрерывно проколотой полоски $M(k)$ в зависимости от числа вилок $k$ для $k>6$.

[anahronizm]

Возможно, сейчас сморожу глупость - не принимайте за умную мысль. А может быть, Вы уже это учитывали.
Итак, каждая следующая вилка "вмещает" в себя предыдущую. Например, первая вилка занимает три клетки (если рассматривать от левого зубца до правого вместе с зубцами), вторая занимает 5 клеток вместе с зубцами (дырка равна 3) и первая вилка целиком помещается в дырку второй вилки. Вторая вилка целиком помещается в дырку третьей вилки и т.д.
Получится ли делать всеми заданными вилками только один проход, организуя остров из проколотых клеток (вилки как бы вложены друг в друга), а вторым проходом организовать другой такой остров. Думаю, можно заранее понять, как выбрать интервал между будущими островами, чтобы он стал заполнен (острова соединились). Останутся только дырки в середине двух островов - как можно заполнить их ?
Ну, это только мысль.
А вот что я хотел бы понять: представим один проход одной (любой) вилкой. Как можно (в виде выражения) описать номера всех не проколотых клеток ?

[waxtep]

anahronizm в сообщении #1718270 писал(а):

Итак, каждая следующая вилка "вмещает" в себя предыдущую. Например, первая вилка занимает три клетки (если рассматривать от левого зубца до правого вместе с зубцами), вторая занимает 5 клеток вместе с зубцами (дырка равна 3) и первая вилка целиком помещается в дырку второй вилки. Вторая вилка целиком помещается в дырку третьей вилки и т.д.
Получится ли делать всеми заданными вилками только один проход, организуя остров из проколотых клеток (вилки как бы вложены друг в друга), а вторым проходом организовать другой такой остров. Думаю, можно заранее понять, как выбрать интервал между будущими островами, чтобы он стал заполнен (острова соединились). Останутся только дырки в середине двух островов - как можно заполнить их ?
Ну, это только мысль.
А вот что я хотел бы понять: представим один проход одной (любой) вилкой. Как можно (в виде выражения) описать номера всех не проколотых клеток ?

У меня была очень похожая визуальная метафора: прогрессии нанизываются на эпицентр, как деревянные кольца разного размера на шест в детской игрушке вроде бы, оптимальные выглядят не так, а скорее похожи на "ключик и скважину" - где у одного набора дырки, у другого зубчики. Для примера шести вилок постил где-то выше картинку одной из (вроде бы) оптимальных стратегий. С другой стороны, может быть, и такая есть, не разглядывал их все внимательно.

Что касается формулы: вилка $i$ в проходе $s$ прокалывает клетки $b_i^s\pm i+n\cdot(6i+2s-3)$, где $b_i^s$ - положение середины этой вилки при каком-то уколе, а $n$ - любое целое число

-- 15.02.2026, 15:06 --

А, Вы хотите формулу для номеров непроколотых клеток $v$. Можно так: $(v-b_i^s\pm i)\not\equiv 0 \mod (6i+2s-3)$

[waxtep]

Или симметрично: вилка $i$ в проходе $s$ не прокалывает клетки $b_i^s\pm i+n\cdot(6i+2s-3)+r$, где $b_i^s$ - положение середины этой вилки при каком-то уколе, $n$ - любое целое число, а $r$ - любое натуральное число от единицы до $6i+2s-4$.

waxtep в сообщении #1718206 писал(а):

пуститься во все тяжкие и попробовать жадные пошаговые стратегии

Должен сказать, здесь пока ничего толкового не вышло, повозился пару вечеров. Здесь Вы совершенно правильно говорите, что

anahronizm в сообщении #1718270 писал(а):

Думаю, можно заранее понять, как выбрать интервал между будущими островами, чтобы он стал заполнен (острова соединились)

и просто так максимизировать какие-то суммарные функции от размеров островков недостаточно. Надо еще обеспечить, чтобы "ключик подошел к скважине", - чтобы проколами оставшихся вилок можно было соединить уже построенные острова. Это тоже наверное можно пробовать формализовать. В целом, мне нравится подход "сначала много подумать и понаписать на бумажке, а уж потом скормить задачу железному коню", а получится ли в данном случае что-то толковое, - посмотрим

[anahronizm]

Меня тоже затянула задачка. Но немного иначе.
Стало интересно попробовать описать все не проколотые элементы при любом заданном количестве вилок. И не обязательно такими вилками, как в задаче.
Вот Вы показали, как можно описать все не проколотые клетки если вилка одна. Удобна ли такая запись при вычислении не проколотых элементов ?
Или вот задача: предположим, что у нас есть бесконечная полоска. И по ней прошлись первой и второй вилкой по два раза (как условие в задаче). Как выразить все не проколотые элементы на этой бесконечной полоске? Да так, чтобы такая запись была удобна для использования, например, вычисления всех не проколотых элементов на заданном интервале.
А если берётся только вторая и третья вилка с их двумя проходами ? Или только пятая, седьмая и восьмая ?
Было бы здорово записать общую формулу.
Или вот ещё: я знаю, что рисунок распределения проколотых (и не проколотых клеток) при любом количестве вилок будет периодичным и симметричным на бесконечной полоске (доказать не умею, но противоречий не вижу). Поэтому при любом начальном расположении вилок на симметричном периоде всегда будет присутствовать минимум две (как я ранее и упоминал) максимальные группы проколотых клеток. Было бы здорово выразить размер такой группы строгой формулой.
Можно и программу написать (наверное).
Для этого проверяем все числа на периоде. Для первых двух вилок период будет равен 5005. Для первых трёх 1616615. Для только второй и третьей 46189.
Проверить на делимость каждый элемент. Для этого представить каждую вилку в виде каждого зуба в отдельности, который с определённой периодичностью прокалывает полоску.
Возможно Вы именно так и делали.
Но, скорее всего, не рассматривали отдельно, например, вилки 2 и 3 или вилки 3,4 и 6.
Жаль, что я не умею писать программы для возможности проверки своих размышлений...

-- 16.02.2026, 10:39 --

Меня тоже затянула задачка. Но немного иначе.
Стало интересно попробовать описать все не проколотые элементы при любом заданном количестве вилок. И не обязательно такими вилками, как в задаче.
Вот Вы показали, как можно описать все не проколотые клетки если вилка одна. Удобна ли такая запись при вычислении не проколотых элементов ?
Или вот задача: предположим, что у нас есть бесконечная полоска. И по ней прошлись первой и второй вилкой по два раза (как условие в задаче). Как выразить все не проколотые элементы на этой бесконечной полоске? Да так, чтобы такая запись была удобна для использования, например, вычисления всех не проколотых элементов на заданном интервале.
А если берётся только вторая и третья вилка с их двумя проходами ? Или только пятая, седьмая и восьмая ?
Было бы здорово записать общую формулу.
Или вот ещё: я знаю, что рисунок распределения проколотых (и не проколотых клеток) при любом количестве вилок будет периодичным и симметричным на бесконечной полоске (доказать не умею, но противоречий не вижу). Поэтому при любом начальном расположении вилок на симметричном периоде всегда будет присутствовать минимум две (как я ранее и упоминал) максимальные группы проколотых клеток. Было бы здорово выразить размер такой группы строгой формулой.
Можно и программу написать (наверное).
Для этого проверяем все числа на периоде. Для первых двух вилок период будет равен 5005. Для первых трёх 1616615. Для только второй и третьей 46189.
Проверить на делимость каждый элемент. Для этого представить каждую вилку в виде каждого зуба в отдельности, который с определённой периодичностью прокалывает полоску.
Возможно Вы именно так и делали.
Но, скорее всего, не рассматривали отдельно, например, вилки 2 и 3 или вилки 3,4 и 6.
Жаль, что я не умею писать программы для возможности проверки своих размышлений...