Лучший алгоритм факторизации чисел

[Dmitriy40]

Skipper в сообщении #1716805 писал(а):

PS mathpath , как вы набираете символ-число возведения в степень, иначем чем в
LaTeX с помощью ^{..} ?

В Unicode есть символы ² (Alt+0178) и ³ (Alt+0179). И много других. В скобках как их можно набрать с клавиатуры. Но за такое будут ругать. Ибо по правилам надо TeX. Тем более когда именно для формул, а не текстов программ.

[Skipper]

Dmitriy40 в сообщении #1716813 писал(а):

Тем более когда именно для формул, а не текстов программ

Спасибо. Просто бывают сложные формулы, а бывают простые. Если там только степени, вот
и "вся сложность", отличающаяся от обычного текста, удобнее же так..

Skipper в сообщении #1716805 писал(а):

Программно не проверял, какая тут вероятность

У Василенко нашёл доказательство, что если нашли два таких квадрата, то вероятность вычислив НОД найти нетривиальный делитель, больше 1/2,
Для кубов не знаю
И в каких случаях находить кубы проще

[mathpath]

Skipper в сообщении #1716805 писал(а):

PS mathpath , как вы набираете символ-число возведения в степень, иначем чем в
LaTeX с помощью ^{..} ? Ваш текст если скопировать то явно удобнее читать,
не переключаясь каждый раз на предпросмотр, без всяких тэгов, спецсимволов и прочего,
прямо в набираемом тексте.

Дипсик свои ответы может выдавать как в латексном, так и в юникодном формате
Для простых формул юникодный формат безусловно проще

[mathpath]

Skipper в сообщении #1716805 писал(а):

Алгоритм Ферма:
Если для числа n мы найдем такие x и y, что:
$x^3 \equiv y^3 (\mod n ) $ (x и y сравнимы по модулю n)
и при этом
x ≠ -y (mod n)
Затем
$x^3 - y^3 \equiv 0 (\mod n )$
То есть разность кубов делится на n , которая раскладывается:
$x^3 - y^3 = (x - y)(x^2 + xy + y^2)$
$(x + y)(x^2 + xy + y^2) $ делится на n ,
Но
$(x + y)$ не делится на n , а с какой то вероятностью, и $(x^2 + xy + y^2)$, не делится на n,
(с какой то вероятностью, может делиться на n) ,
значит, если в случае, когда оба не делятся, то с какой то вероятностью получим,
1 < НОД(n, x + y) < n ,
Тогда, этот НОД , даст первый нетривиальный делитель n , а второй, если подставить трехчлен,

Или я что-то тут неправильно понял?

Неправильно разложена на множители разность кубов:
Правильная формула:
x³−y³=(x−y)(x²+xy+y²)

В формуле разности кубов нет множителя (x+y) вообще.

[Skipper]

mathpath в сообщении #1716836 писал(а):

Неправильно разложена на множители разность кубов:
Правильная формула:
x³−y³=(x−y)(x²+xy+y²)

Ничего не меняет, суть та же.
Вот уточнил- изменив плюс на минус:

Алгоритм Ферма:
Если для числа n мы найдем такие x и y, что:
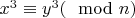
$x^3 \equiv y^3 (\mod n ) $ (x и y сравнимы по модулю n)
и при этом
x ≠ y (mod n)
Затем
$x^3 - y^3 \equiv 0 (\mod n )$
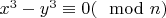
То есть разность кубов делится на n , которая раскладывается:
$x^3 - y^3 = (x - y)(x^2 + xy + y^2)$
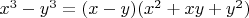
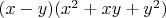
$(x - y)(x^2 + xy + y^2) $ делится на n ,
Но
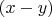
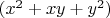
$(x - y)$ не делится на n , а с какой то вероятностью, и $(x^2 + xy + y^2)$, не делится на n,
(с какой то вероятностью, может делиться на n) ,
значит, если в случае, когда оба не делятся, то с какой то вероятностью получим,
1 < НОД(n, x - y) < n ,
Тогда, этот НОД , даст первый нетривиальный делитель n , а второй, если подставить трехчлен,

PS "то с какой то вероятностью получим" - для разности квадратов, эта вероятность больше 1/2,
доказательство видел в книге Василенко. Если в случае с кубами (а скорее всего так и есть),
то же самое с приемлемой точностью, то принцип факторизации тот же.
Значит если найти случаи, что с кубами быстрее алгоритм где то будет работать,
(не знаю, может быть, метод просеивания, или более быстрое нахождение "B-гладких чисел",
или часть алгоритма в шаге линейной алгебры, и т.п.), то весь принцип с кубами
может оказаться быстрее чем с квадратами, и мы улучшили бы ECM, SIQS, GNFS ,
Просто интересное наблюдение, но нигде не видел каких то исследований по этому поводу

[mathpath]

Skipper в сообщении #1716837 писал(а):

$x^3 - y^3 \equiv 0 (\mod n )$
То есть разность кубов делится на n , которая раскладывается:
$x^3 - y^3 = (x - y)(x^2 + xy + y^2)$
$(x - y)(x^2 + xy + y^2) $ делится на n ,
Но
$(x - y)$ не делится на n , а с какой то вероятностью, и $(x^2 + xy + y^2)$, не делится на n,
(с какой то вероятностью, может делиться на n) ,
значит, если в случае, когда оба не делятся, то с какой то вероятностью получим,
1 < НОД(n, x - y) < n ,
Тогда, этот НОД , даст первый нетривиальный делитель n , а второй, если подставить трехчлен,

PS "то с какой то вероятностью получим" - для разности квадратов, эта вероятность больше 1/2,
доказательство видел в книге Василенко.

Если (x−y)(x²+xy+y²)≡0(modn)
и.
x−y≡ ̸0(modn)
то это не значит, что x−y не делится ни на один делитель n.

На самом деле, ровно наоборот: чтобы произведение делилось на n, каждый простой делитель n должен делить хотя бы один из множителей..
Если x−y не делится на n целиком, но делится на какой-то подмножество простых делителей n, то на остальные делители n должно делиться x²+xy+y².

Если (x−y)(x²+xy+y²)≡0(modn)
и.
x−y≡ ̸0(modn)
то это не значит, что x−y не делится ни на один делитель n.

Ваш «алгоритм» правильно математически говорит, что если найдутся такие x,yx,y, то можно факторизовать n..
Но проблема в том, как их найти.

Если мы просто будем перебирать x,yx,y, то проверка x³≡y³(modn) — это та же сложность, что и факторизация «в лоб»..
Это не алгоритм Ферма.

[Skipper]

mathpath в сообщении #1716838 писал(а):

На самом деле, ровно наоборот: чтобы произведение делилось на n, каждый простой делитель n должен делить хотя бы один из множителей..

А это что?

mathpath в сообщении #1715242 писал(а):

То есть n делит разность квадратов, которая раскладывается:
x² - y² = (x + y)(x - y)
n | (x + y)(x - y)
Но
n ∤ (x - y) и n ∤ (x + y)

В вашем сообщении- произведение делится на n, но ни один из множителей произведения на n не делится.
Только у вас фраза "n делит что то там..", а у меня более удобная мне "что то там делится на n".

-- Вс фев 01, 2026 08:38:12 --

mathpath в сообщении #1716838 писал(а):

то на остальные делители n должно делиться x²+xy+y².

И что с того? Ваш пример с квадратами абсолютно эквивалентен примеру с кубами.
Получили произведение у меня например (x-y) (...что-то там...) - и оно делится на N.
Пусть (x-y) (...что-то там...) == 90, а N = 10 которое надо факторизовать.

Может быть такое что ни один из множителей произведения на 10 не делится (хотя само произведение делится, ведь 90 делится на 10).
Вот,
(x-y) (...что-то там...) == 2 * 45 .

Именно потому что ни один из множителей произведения не делится на 10, то есть ни 2, ни 45,
находя НОД-ы, мы и разложим число N = 10 на множители.

НОД(10, 2) = 2,
НОД(10, 45) = 5,

В чем тогда вы усматритваете тут разницу между разложением (x-y) (...что-то там...) ,
точнее,
(x-y) (x+y)
и в случае
(x-y) (x²+xy+y²)

Принцип абсолютно тот же..

-- Вс фев 01, 2026 08:41:11 --

mathpath в сообщении #1716838 писал(а):

Если мы просто будем перебирать x,yx,y, то проверка x³≡y³(modn) — это та же сложность, что и факторизация «в лоб»..

Ничего там перебирать в лоб не надо, кроме как искать кубы равные по модулю,
так же как ищем квадраты.
В случае квадратов с вероятностью 1/2 или больше, оба множителя не будут делиться на N,
в случае кубов что то подобное, найдя не первый так второй, или третий... мы и факторизуем число,

[mathpath]

Если x³≡y³(mod n) и x≢y(mod n), то gcd⁡(n,x−y) будет НЕТРИВИАЛЬНЫМ делителем