1. В ней может быть левый нейтральный, но не быть правого нейтрального.
Контрпример привести что ли?
1. Пусть на множестве задана операция и есть левый нейтральный по такой операции элемент

.
1.1 Любой элемент в паре с нейтральным справа ставится такой операцией в соответствие константе

:
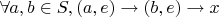
1.2 А также любой элемент в паре с такой константой

(в любом порядке) ставится в соответствие этой же константе:
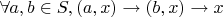
(не противоречит 1.1 и не противоречит определению левого нейтрального элемента, который есть).
2.Такое правило не мешает операции быть ассоциативной:
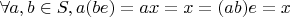
. Для остальных наборов
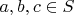
полагаем ассоциативность аксиоматичной, к противоречию это не приводит. Значит такая операция может быть ассоциативной
3. Пусть
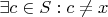
, тогда по п.2 нейтральный слева, будучи расположенным справа для такого

не будет нейтральным. Значит есть левый нейтральный, который справа не нейтрален хотя бы для одного элемента
4. Значит существует полугруппа с левым нейтральным, но без правого.
Или как-то более обобщающе это доказывается?
Upd: необходимо уточнить до

, иначе с
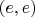
возникает противоречие.