Нашёл доказательство того, что любой элемент должен быть левым обратным. Это переиспользование части общего доказательства из сообщения выше, которая, кстати, тоже была не полностью верна. Предыдущее доказательство пожалуйста игнорируйте.
От обратного: пускай в полугруппе есть левый нейтральный

и для каждого есть левый обратный, но существует элемент

, который сам левым обратным ни к кому не является.
I. По условию, тем не менее у

есть левый обратный

. Тогда можно утверждать что
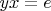
, но
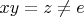
- поскольку, раз

не является ни для кого левым обратным, но и в том числе для своего левого обратного.
Тогда

, но
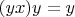
, следовательно
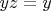
, но

.
Таким образом

Значит для соблюдения ассоциативности любой левый обратный (который есть у всех по условию) в паре с парой: слева - элемента к которому он явл. левым обратным; справа - он сам (левый обратный), должен отображаться в себя т.е.
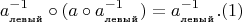
А это значит, что пара любого элемента расположенного слева со своим обратным слева, расположенным справа, т.е.
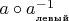
обязана быть равна правому нейтральному, ну или левому

, поскольку существования правого мы ещё не доказали?
Вообще-то нет.
Может быть для каждого элемента

, пара

хоть и отображает
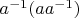
в

, но она разная для каждого

, не равна левому нейтральному, а значит не подходит под определение правого нейтрального, а значит и

не является левым обратным к

, что мы в итоге и хотим получить.
II. И вот спустя четыре часа, доказательство, что если
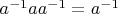
, то

обязано быть левым обратным я нашёл. А точнее даже более сильное утверждение - для любого

,
имеющего левый обратный, если

, то

- левый нейтральный. Доказательство:
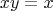
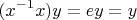
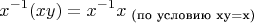

Тогда
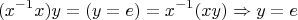 III.
III. Таким образом, возвращаясь к

,
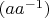
обязано быть левым нейтральным, а значит для любого левого обратного

, который по условию есть у любого

, существует свой левый обратный - этот же

, а значит не только у любого элемента есть левый обратный, но и
любой элемент является левым обратным (своего левого обратного), Ч.Т.Д.
Самое ироничное что это и доказательство
всего утверждения - поскольку:
1) Тот факт, что каждый элемент является левым обратным к своему левому обратному означает что у каждого элемента есть правый обратный - Ч.Т.Д.
2) А доказательство существования правого нейтрального, с учётом доказанности верхнего пункта - фактически в секции
II - Ч.Т.Д.
(Оффтоп)
Именно что для конечного. А утверждение верно и для бесконечных полугрупп
Кстати, это доказательство теперь не зависит от мощности множества.