Someone
Итак, имеем 3 системы линейных уравнений по 3 уравнения в каждой - итого 9 уравнений.
В них имеем 9 известных величин и ( 9 компонент искомой матрицы и 9 компонент неизвестных векторов =18 ) 18 неизвестных величин.
Я надеялся 9 неизвестных векторов заменить произведением обратной матрицы и известных векторов - тогда бы получилось 9 компонент искомой матрицы.
Понятно обьяснил ?
Я прав в своих надеждах ?
Вам всё время твердят, что в вашей задаче

уравнений и

(!) неизвестных. Максимум, что Вы можете сделать — выразить

неизвестных через оставшиеся

, которые придётся "взять с потолка".
Вам неоднократно предлагали взять произвольную невырожденную матрицу

. Проще всего — единичную:
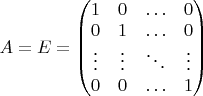
. Тогда из
уравнения 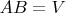
можно найти матрицу
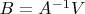
.
Другой удобный вариант — задать произвольно векторы

так, чтобы получилась невырожденная матрица

(проще всего —

). Тогда из того же уравнения можно будет найти
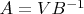
.
Что Вам во всём этом непонятно?