Обратная задача матричного исчисления

[pan555]

Добрый день!
Кто либо занимался задачей, которую можно назвать :"Обратная задача матричного исчисления" ?
Ибо обычно задана матрица n×n , на которую умножают вектор n-го размера и получают нужный вектор ,тоже n-го размера.
У меня же есть n векторов размера n ,полученных экспериментально - и по этой информации надо восстановить матрицу n×n.
Такую задачу кто либо ставил ?

[mihaild]

pan555 в сообщении #1714538 писал(а):

У меня же есть n векторов размера n ,полученных экспериментально - и по этой информации надо восстановить матрицу n×n

А как эти вектора должны быть связаны с матрицей?

[pan555]

mihaild в сообщении #1714542 писал(а):

pan555 в сообщении #1714538 писал(а):

У меня же есть n векторов размера n ,полученных экспериментально - и по этой информации надо восстановить матрицу n×n

А как эти вектора должны быть связаны с матрицей?

Например , известен вектор v1 размера n - есть результат умножения матрицы A на неизвестный вектор b1.
И таких известных векторов n штук : v1...vn, им соответствуют n штук неизвестных векторов b1...bn,
а матрица, которую надо найти A (n×n)-одна и та же.

[mihaild]

Ага, т.е. всё-таки не просто $n$ векторов, а $n$ пар векторов.
Да, эта задача известна, называется "решение системы линейных уравнений".
Обратите внимание, что в данном случае система легко разбивается на $n$ отдельных систем - понимаете, каких?

[Someone]

pan555 в сообщении #1714548 писал(а):

Например , известен вектор v1 размера n - есть результат умножения матрицы A на неизвестный вектор b1.
И таких известных векторов n штук : v1...vn, им соответствуют n штук неизвестных векторов b1...bn,
а матрица, которую надо найти A (n×n)-одна и та же.

Да возьмите любую невырожденную матрицу $A$ размера $n\times n$… И по известным векторам с помощью этой матрицы найдите неизвестные.

[pan555]

mihaild в сообщении #1714549 писал(а):

Ага, т.е. всё-таки не просто $n$ векторов, а $n$ пар векторов.
Да, эта задача известна, называется "решение системы линейных уравнений".
Обратите внимание, что в данном случае система легко разбивается на $n$ отдельных систем - понимаете, каких?

Почему пар векторов?
У меня - n известных векторов размера n для результата умножения искомой матрицы n×n на неизвестные
n векторов размера n.

-- 12.01.2026, 19:49 --

Someone в сообщении #1714550 писал(а):

pan555 в сообщении #1714548 писал(а):

Например , известен вектор v1 размера n - есть результат умножения матрицы A на неизвестный вектор b1.
И таких известных векторов n штук : v1...vn, им соответствуют n штук неизвестных векторов b1...bn,
а матрица, которую надо найти A (n×n)-одна и та же.

Да возьмите любую невырожденную матрицу $A$ размера $n\times n$… И по известным векторам с помощью этой матрицы найдите неизвестные.

И каа вы это предлагаете практически сделать ?
Хотя бы на примере матрицы 3×3 ?

[mihaild]

pan555 в сообщении #1714552 писал(а):

У меня - n векторов размера n для матрицы n×n

pan555 в сообщении #1714548 писал(а):

И таких известных векторов n штук : v1...vn, им соответствуют n штук неизвестных векторов b1...bn

Т.е. у вас пары $(v_1, b_1)$, $(v_2, b_2)$ и т.д.

pan555 в сообщении #1714552 писал(а):

И каа вы это предлагаете практически сделать ?

У вас есть $n^2$ неизвестных - коэффициенты $a_{ij}$. И уравнения вида $A v_i = b_i$. Расписав произведение матрицы на вектор по определению через компоненты векторов и эти неизвестные, составьте систему уравнений.

[dgwuqtj]

pan555 в сообщении #1714548 писал(а):

И таких известных векторов n штук : v1...vn, им соответствуют n штук неизвестных векторов b1...bn,
а матрица, которую надо найти A (n×n)-одна и та же.

Так возьмите $b_i = v_i$, а матрицу $A$ единичную.

[pan555]

mihaild в сообщении #1714554 писал(а):

pan555 в сообщении #1714552 писал(а):

У меня - n векторов размера n для матрицы n×n

pan555 в сообщении #1714548 писал(а):

И таких известных векторов n штук : v1...vn, им соответствуют n штук неизвестных векторов b1...bn

Т.е. у вас пары $(v_1, b_1)$, $(v_2, b_2)$ и т.д.

pan555 в сообщении #1714552 писал(а):

И каа вы это предлагаете практически сделать ?

У вас есть $n^2$ неизвестных - коэффициенты $a_{ij}$. И уравнения вида $A v_i = b_i$. Расписав произведение матрицы на вектор по определению через компоненты векторов и эти неизвестные, составьте систему уравнений.

Точнее, уравнения вида $A* b_i = v_i$,таких уравнений $n^2$ штук
Известны только величины $ v_i = v_1...v_n$, а величины $b_i = b_1..b_n$, могу через известные величины $v_i = v_1...v_i)n$, выразить через обратную к матрице $A$ матрицу и тогда получу $n^2$ уравнений для $n^2$ неизвестных.
Я правильно понимаю ?

-- 12.01.2026, 20:27 --

dgwuqtj в сообщении #1714563 писал(а):

pan555 в сообщении #1714548 писал(а):

И таких известных векторов n штук : v1...vn, им соответствуют n штук неизвестных векторов b1...bn,
а матрица, которую надо найти A (n×n)-одна и та же.

Так возьмите $b_i = v_i$, а матрицу $A$ единичную.

Думаю, вы невнимательро посмотрели исходную задачу.

[mihaild]

pan555 в сообщении #1714565 писал(а):

Точнее, уравнения вида $A* b_i = v_i$,таких уравнений $n^2$ штук

Произведение в этом контексте звездочкой не обозначается. Либо $\cdot$, либо вообще ниычего.

pan555 в сообщении #1714565 писал(а):

а величины $b_i = b_1..b_n$, могу через известные величины $v_i = v_1...v_i)n$, выразить через обратную к матрице $A$ матрицу

Кто на ком стоял? (что через что выразить?)

Если $b_i$ и $v_i$ известны, то обратная к $A$ матрица Вам не нужна.
Вообще, если сделать матрицу $B$, в которой по столбцам стоят $b_i$, и матрицу $V$, в которой по столбцам стоят $v_i$, то набор равенств $A b_i = v_i$ можно красиво симметрично записать как $AB = V$. Можно задать любые две матрицы из этих трех, и искать третью.

[pan555]

mihaild в сообщении #1714568 писал(а):

pan555 в сообщении #1714565 писал(а):

Точнее, уравнения вида $Ab_i = v_i$,таких уравнений $n^2$ штук

Произведение в этом контексте звездочкой не обозначается. Либо $\cdot$, либо вообще ниычего.

pan555 в сообщении #1714565 писал(а):

а величины $b_i = b_1..b_n$, могу через известные величины $v_i = v_1...v_in$, выразить через обратную к матрице $A$ матрицу

Кто на ком стоял? (что через что выразить?)

Если $b_i$ и $v_i$ известны, то обратная к $A$ матрица Вам не нужна.
Вообще, если сделать матрицу $B$, в которой по столбцам стоят $b_i$, и матрицу $V$, в которой по столбцам стоят $v_i$, то набор равенств $A b_i = v_i$ можно красиво симметрично записать как $AB = V$. Можно задать любые две матрицы из этих трех, и искать третью.

В том то и дело, что известны только $v_i$ , поэтому обратная матрица нужна.
И даже если мы получим $n^2$ уравнений с $n^2$ неизвестными,
то эти ураврпния будут таковы, где эти неизвестные перемножатся между собой, а то и будут,как минимум, их квадраты, а то и кубы и т.п. и задача усложнится. Это надо исследовать..

[mihaild]

pan555 в сообщении #1714576 писал(а):

В том то и дело, что известны только $v_i$

Тогда решений много. Для любой невырожденной $A$ есть ровно одно решение. Если $V$ вырождена, то и для некоторых вырожденных $A$ тоже есть.

pan555 в сообщении #1714576 писал(а):

Это надо исследовать

В этой области всё исследовано очень подробно, если сформулировать что Вы собственно хотите.

[pan555]

mihaild в сообщении #1714577 писал(а):

pan555 в сообщении #1714576 писал(а):

В том то и дело, что известны только $v_i$

Тогда решений много. Для любой невырожденной $A$ есть ровно одно решение. Если $V$ вырождена, то и для некоторых вырожденных $A$ тоже есть.

pan555 в сообщении #1714576 писал(а):

Это надо исследовать

В этой области всё исследовано очень подробно, если сформулировать что Вы собственно хотите.

Считаем, что матрица $A$ НЕ вырождена.
В таком случае есть обратная матрица и мы приходим к выше описанной системе уравнений.
Вопрос с том, какие они будут...
Задача, кстати , поставлена для квадратных матриц.
А если иметь вектора размером п и матрицу n×m и иметь m известнвх векторов размера n. ,которые есть результат умножения, то имеется ли для такого расширения задачи решение ?
Думаю, вопрос упрётся в то, что насколько я знаю, для матриц m×n нет обратных матриц.
Или я ошибаюсь?

[mihaild]

pan555 в сообщении #1714580 писал(а):

В таком случае есть обратная матрица и мы приходим к выше описанной системе уравнений.
Вопрос с том, какие они будут

Да зачем вам обратная матрица? У вас квадратичная система с $2n^2$ неизвестными (легко выписывается по определению). Решений у неё много.

pan555 в сообщении #1714580 писал(а):

А если иметь вектора размером п и матрицу n×m и иметь m известнвх векторов размера n. ,которые есть результат умножения, то имеется ли для такого расширения задачи решение ?

Самостоятельные попытки решения?

[Someone]

pan555 в сообщении #1714552 писал(а):

Someone в сообщении #1714550 писал(а):

pan555 в сообщении #1714548 писал(а):

Например , известен вектор v1 размера n - есть результат умножения матрицы A на неизвестный вектор b1.
И таких известных векторов n штук : v1...vn, им соответствуют n штук неизвестных векторов b1...bn,
а матрица, которую надо найти A (n×n)-одна и та же.

Да возьмите любую невырожденную матрицу $A$ размера $n\times n$… И по известным векторам с помощью этой матрицы найдите неизвестные.

И каа вы это предлагаете практически сделать ?
Хотя бы на примере матрицы 3×3 ?

Что значит — как? Как на первом курсе учили. Разные способы есть. Например, можно обратную матрицу вычислить, но это очень громоздкий способ. Или по формулам Крамера решать, но это, наверное, ещё хуже будет. Или метод Гаусса применить.
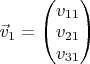
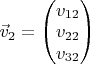
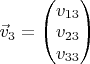
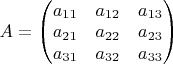
Ну, пусть у нас заданы векторы $\vec v_1=\begin{pmatrix}v_{11}\\ v_{21}\\ v_{31}\end{pmatrix}$, $\vec v_2=\begin{pmatrix}v_{12}\\ v_{22}\\ v_{32}\end{pmatrix}$, $\vec v_3=\begin{pmatrix}v_{13}\\ v_{23}\\ v_{33}\end{pmatrix}$. Неизвестная матрица пусть есть $A=\begin{pmatrix}a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{33}\end{pmatrix}$, а неизвестные векторы — $\vec b_1=\begin{pmatrix}b_{11}\\ b_{21}\\ b_{31}\end{pmatrix}$, $\vec b_2=\begin{pmatrix}b_{12}\\ b_{22}\\ b_{32}\end{pmatrix}$, $\vec b_3=\begin{pmatrix}b_{13}\\ b_{23}\\ b_{33}\end{pmatrix}$.
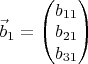
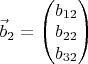
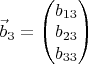
Как я предлагал, матрицу $A$ заполняем любыми числами (нужно проверить, что определитель не равен $0$). Как советовал dgwuqtj, лучше всего в качестве $A$ взять единичную матрицу. Тогда будет просто $\vec b_1=\vec v_1$, $\vec b_2=\vec v_2$, $\vec b_3=\vec v_3$.

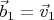
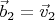
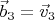
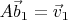
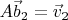
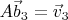
Дальше либо записываем три матричных уравнения $A\vec b_1=\vec v_1$, $A\vec b_2=\vec v_2$, $A\vec b_3=\vec v_3$, либо записываем их в виде трёх систем по три линейных уравнения
$\begin{cases}a_{11}b_{11}+a_{12}b_{21}+a_{13}b_{31}=v_{11},\\ a_{21}b_{11}+a_{22}b_{21}+a_{23}b_{31}=v_{21},\\ a_{31}b_{11}+a_{32}b_{21}+a_{33}b_{31}=v_{31},\end{cases}$    $\quad\begin{cases}a_{11}b_{12}+a_{12}b_{22}+a_{13}b_{32}=v_{12},\\ a_{21}b_{12}+a_{22}b_{22}+a_{23}b_{32}=v_{22},\\ a_{31}b_{12}+a_{32}b_{22}+a_{33}b_{32}=v_{32},\end{cases}$    $\quad\begin{cases}a_{11}b_{13}+a_{12}b_{23}+a_{13}b_{33}=v_{13},\\ a_{21}b_{13}+a_{22}b_{23}+a_{23}b_{33}=v_{23},\\ a_{31}b_{11}+a_{32}b_{21}+a_{33}b_{31}=v_{33}.\end{cases}$
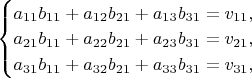
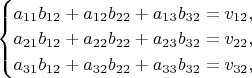
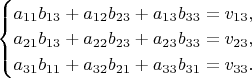
И решаем их любым известным Вам способом.

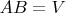
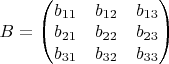
А можно объединить их в одно матричное уравнение $AB=V$, где $B=\begin{pmatrix}b_{11}&b_{12}&b_{13}\\ b_{21}&b_{22}&b_{23}\\ b_{31}&b_{32}&b_{33}\end{pmatrix}$ и $V=\begin{pmatrix}v_{11}&v_{12}&v_{13}\\ v_{21}&v_{22}&v_{23}\\ v_{31}&v_{32}&v_{33}\end{pmatrix}$ и решить его любым известным Вам способом (лучше всего — методом Гаусса).