Доказательство. Пусть
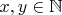
(натуральные, то есть положительные) удовлетворяют

Правая часть равна
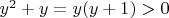
. Так как

, из (1) следует, что
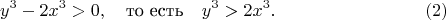
В частности,

.
Преобразуем (1):



Докажем, что множители в левой части (5) взаимно просты. Обозначим

Тогда

, а также
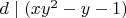
. Но по модулю

имеем
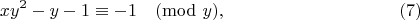
следовательно, из

и
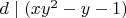
получаем
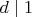
, то есть

\textbf{Лемма.} Пусть
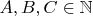
,
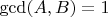
и

Тогда существуют
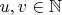
и

такие, что

\textit{Доказательство леммы.}
Рассмотрим разложение

на простые:
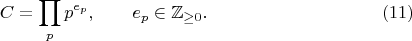
Тогда
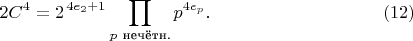
Так как
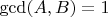
, каждый простой

входит целиком либо в

, либо в

(в смысле: его степень в произведении

целиком принадлежит одному из множителей). Для нечётного простого

степень
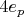
кратна

, значит, в том множителе (

или

), куда попал

, показатель степени

кратен

; следовательно, нечётная часть каждого из

и

является четвёртой степенью.
Для простого

суммарный показатель в (12) равен
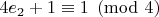
, а поскольку

и

взаимно просты, вся степень двойки
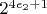
попадает либо в

, либо в

. Значит, один из множителей равен

умножить на четвёртую степень, а другой — просто четвёртая степень.
Формально: положим

, если
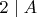
, и

, если
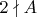
(тогда обязательно
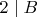
). Определим

как произведение тех простых

, которые попали в

, с показателями

, а

— как произведение остальных простых (попавших в

) тоже с показателями

. Тогда по построению
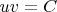
, и из (12) получаем представление (10). Лемма доказана.
Применим лемму к (5) с

Условие
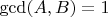
выполнено по (8), а равенство

— это (5). Следовательно, существуют
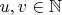
и

такие, что
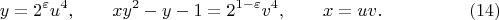
Рассмотрим два случая.
\textbf{Случай 1:

.}
Тогда из (14)
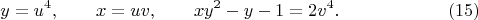
Так как по (2)

, получаем

, то есть

Подставим

,
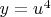
в равенство
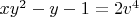
:
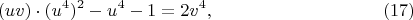
то есть

или, вынеся

,

Обозначим

Тогда из (19) имеем
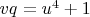
, в частности,

Покажем, что

. Предположим противное:
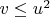
. Тогда
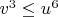
, и потому
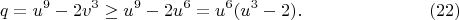
Для
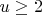
имеем
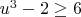
, значит из (22)

Тогда из (19), учитывая
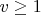
,
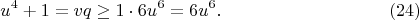
Но при
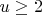
выполняется
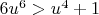
(например,
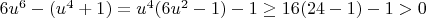
), противоречие. Следовательно,

Из (25) следует
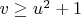
, поэтому

а значит, из
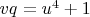
получаем

Кроме того, из (25) и (16) имеем

.
Теперь используем сравнение по модулю

. Из (21) следует

Возведём (28) в квадрат:

и умножим на

:

По определению
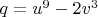
, а
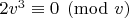
, поэтому из (30)

Но по (27)
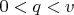
, а также
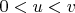
. Из (31) следует, что
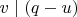
.
Так как
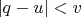
, единственная возможность —

, то есть

Тогда из
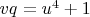
получаем
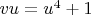
, то есть

Но
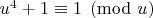
, значит (33) возможно только при

, что противоречит (16). Следовательно, случай

невозможен.
\textbf{Случай 2:

.}
Тогда из (14)
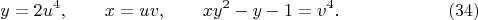
Подставим

,
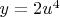
в равенство
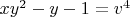
:
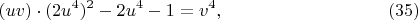
то есть

Перепишем (36) в виде

Обозначим

Тогда из (37) имеем

, в частности,

Докажем, что при
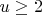
обязательно

. Предположим противное:
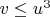
.
Тогда
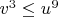
, и потому из (38)
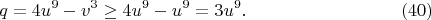
Тогда из (37), учитывая
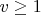
,
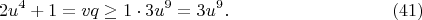
Но при
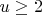
имеем
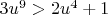
(например,
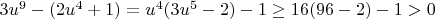
), противоречие. Значит, при
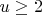

Пусть теперь
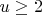
. Тогда из (37) и (42) получаем оценку на

:
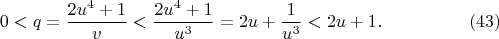
При
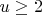
выполнено
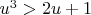
(так как

), и из (42) следует
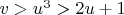
.
Совместно с (43) это даёт
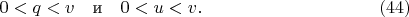
Теперь найдём

по модулю

. Из (39) имеем
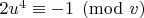
, умножая на
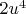
:

и умножая на

:

По определению
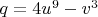
, а
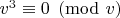
, значит из (46)

Из (44) следует
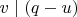
и
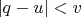
, поэтому
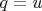
, то есть

Тогда из

получаем
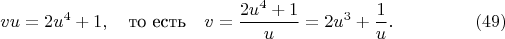
Правая часть целая тогда и только тогда, когда

, то есть

, что противоречит предположению
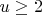
. Значит,

Подставляя

в (37), получаем

Так как

, из (51) следует
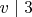
, то есть
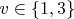
. При

левая часть равна
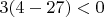
, что невозможно, следовательно

По (34) имеем
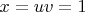
и
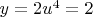
, то есть найдено решение

.
Осталось проверить, что оно действительно удовлетворяет (1):

Итак, случай

невозможен, а в случае

единственно возможно

,

, что даёт

.
Следовательно, уравнение (1) имеет ровно одно решение в натуральных числах:
