|
Последний раз редактировалось Dmitriy40 04.01.2026, 10:33, всего редактировалось 1 раз.
И что после этого программа будет делать, переключится на поиск 45-значных, по системе выше? Да, если указать соответствующий pretest-ratio, то переключится. Либо переключится на SIQS/GNFS. Не могу понять, с какой же вероятностью, может такое быть что будут пройдены все 2350 кривых, и факторизовать не получится? С какой-то ненулевой. Я выше приводил цитату про вероятность 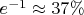 , но учитывая что проверяются ещё и все меньшие кривые, она заметно ниже. Но точно не нулевая, вот например несколько запусков на одном и том же числе:
82049548511544548685847575944819807072619055726693=9054322205635625129311769*9061920555519325508797997
01/04/26 09:41:03, prp25 = 9061920555519325508797997 (curve 79 stg2 B1=50000 sigma=2325151931 thread=2)
01/04/26 09:41:18, prp25 = 9061920555519325508797997 (curve 119 stg2 B1=50000 sigma=3330506305 thread=2)
01/04/26 09:41:25, prp25 = 9061920555519325508797997 (curve 46 stg2 B1=50000 sigma=3491928577 thread=1)
01/04/26 09:41:45, prp25 = 9054322205635625129311769 (curve 27 stg2 B1=50000 sigma=2961887835 thread=0)
01/04/26 09:41:53, prp25 = 9054322205635625129311769 (curve 183 stg2 B1=50000 sigma=332919070 thread=3)
01/04/26 09:42:00, prp25 = 9054322205635625129311769 (curve 67 stg2 B1=50000 sigma=2939750673 thread=1)
01/04/26 09:42:06, prp25 = 9061920555519325508797997 (curve 91 stg2 B1=50000 sigma=1889971066 thread=0)
01/04/26 09:42:50, prp25 = 9061920555519325508797997 (curve 78 stg2 B1=50000 sigma=772172095 thread=0)
01/04/26 09:43:03, prp25 = 9054322205635625129311769 (curve 36 stg2 B1=250000 sigma=3395558366 thread=0)
01/04/26 09:55:31, prp25 = 9054322205635625129311769 (curve 206 stg2 B1=50000 sigma=939127073 thread=0)
01/04/26 09:55:49, prp25 = 9054322205635625129311769 (curve 134 stg2 B1=50000 sigma=2568758773 thread=0)
01/04/26 09:55:57, prp25 = 9061920555519325508797997 (curve 205 stg2 B1=50000 sigma=2223103029 thread=1)
01/04/26 09:56:04, prp25 = 9054322205635625129311769 (curve 148 stg2 B1=50000 sigma=1726755673 thread=1)
01/04/26 09:56:10, prp25 = 9061920555519325508797997 (curve 135 stg2 B1=50000 sigma=3659200596 thread=0)
01/04/26 09:56:16, prp25 = 9061920555519325508797997 (curve 112 stg2 B1=50000 sigma=1821413870 thread=0)
01/04/26 09:56:22, prp25 = 9054322205635625129311769 (curve 114 stg2 B1=50000 sigma=1459448008 thread=0)
01/04/26 09:56:29, prp25 = 9054322205635625129311769 (curve 190 stg2 B1=50000 sigma=2446945114 thread=2)
01/04/26 09:56:41, prp25 = 9061920555519325508797997 (curve 107 stg2 B1=50000 sigma=1651878075 thread=1)
01/04/26 09:56:44, prp25 = 9054322205635625129311769 (curve 14 stg1 B1=50000 sigma=2106432520 thread=1)
01/04/26 09:57:10, prp25 = 9054322205635625129311769 (curve 82 stg2 B1=50000 sigma=2396675142 thread=3)
01/04/26 09:57:17, prp25 = 9061920555519325508797997 (curve 11 stg2 B1=50000 sigma=2548865428 thread=0)
01/04/26 09:57:25, prp25 = 9054322205635625129311769 (curve 204 stg2 B1=50000 sigma=3150896953 thread=3)
01/04/26 09:57:31, prp25 = 9054322205635625129311769 (curve 129 stg2 B1=50000 sigma=2612395811 thread=2)
01/04/26 09:57:34, prp25 = 9061920555519325508797997 (curve 17 stg2 B1=50000 sigma=2777112727 thread=0)
01/04/26 09:57:38, prp25 = 9061920555519325508797997 (curve 47 stg1 B1=50000 sigma=695682415 thread=0)
01/04/26 09:57:41, prp25 = 9061920555519325508797997 (curve 9 stg2 B1=50000 sigma=3819061399 thread=2)
01/04/26 09:57:44, prp25 = 9054322205635625129311769 (curve 35 stg1 B1=11000 sigma=3783068911 thread=3)
01/04/26 09:57:48, prp25 = 9054322205635625129311769 (curve 42 stg2 B1=11000 sigma=2802301583 thread=3)
01/04/26 09:57:52, prp25 = 9061920555519325508797997 (curve 47 stg2 B1=50000 sigma=987771092 thread=0)
01/04/26 09:58:15, prp25 = 9061920555519325508797997 (curve 142 stg2 B1=50000 sigma=2583591192 thread=3)
01/04/26 09:58:23, prp25 = 9061920555519325508797997 (curve 29 stg2 B1=50000 sigma=1579250619 thread=2)
01/04/26 09:58:28, prp25 = 9061920555519325508797997 (curve 77 stg2 B1=50000 sigma=1792006335 thread=2)
01/04/26 09:58:31, prp25 = 9061920555519325508797997 (curve 25 stg2 B1=50000 sigma=2240729133 thread=2)
01/04/26 09:58:38, prp25 = 9061920555519325508797997 (curve 158 stg2 B1=50000 sigma=1972067623 thread=1)
01/04/26 09:58:40, prp25 = 9061920555519325508797997 (curve 27 stg2 B1=11000 sigma=394482280 thread=1)
01/04/26 09:58:42, prp25 = 9061920555519325508797997 (curve 28 stg2 B1=11000 sigma=297852996 thread=0)
01/04/26 09:58:47, prp25 = 9061920555519325508797997 (curve 103 stg2 B1=50000 sigma=2595524870 thread=3)
01/04/26 09:58:58, prp25 = 9061920555519325508797997 (curve 14 stg2 B1=250000 sigma=1349056870 thread=2)
Как видите на 9-й и 38-й раз не смогла найти 25-значный делитель и переключилась на 30-значные. А четыре раза из 38 нашла делитель и при проверке 20-значных. Если Вам так хочется проверять именно методом ECM, да ещё и знаете какой должен быть делитель, то запускайте сразу ECM примерно так: yafu-x64.exe "ecm(82049548511544548685847575944819807072619055726693,214)" -B1ecm 50000214 здесь это количество кривых, хотите до упора - ставьте побольше (миллионы) и ждите. Вот например 100 запусков с 9999 кривыми, смотрите сколько раз она не смогла найти делитель за 214 кривых:
01/04/26 10:11:31, prp25 = 9061920555519325508797997 (curve 321 stg2 B1=50000 sigma=2887846600 thread=0)
01/04/26 10:11:49, prp25 = 9061920555519325508797997 (curve 95 stg1 B1=50000 sigma=3670268364 thread=0)
01/04/26 10:12:19, prp25 = 9054322205635625129311769 (curve 85 stg2 B1=50000 sigma=1383497602 thread=1)
01/04/26 10:12:30, prp25 = 9054322205635625129311769 (curve 402 stg2 B1=50000 sigma=2920941997 thread=3)
01/04/26 10:12:36, prp25 = 9054322205635625129311769 (curve 56 stg2 B1=50000 sigma=3027557850 thread=3)
01/04/26 10:12:42, prp25 = 9054322205635625129311769 (curve 21 stg2 B1=50000 sigma=2364868216 thread=3)
01/04/26 10:12:49, prp25 = 9054322205635625129311769 (curve 214 stg2 B1=50000 sigma=1486926279 thread=3)
01/04/26 10:12:52, prp25 = 9054322205635625129311769 (curve 7 stg2 B1=50000 sigma=2827444491 thread=2)
01/04/26 10:12:57, prp25 = 9054322205635625129311769 (curve 117 stg1 B1=50000 sigma=3719216325 thread=1)
01/04/26 10:13:05, prp25 = 9061920555519325508797997 (curve 224 stg2 B1=50000 sigma=3603148958 thread=1)
01/04/26 10:13:21, prp25 = 9054322205635625129311769 (curve 68 stg2 B1=50000 sigma=2919202363 thread=1)
01/04/26 10:13:32, prp25 = 9054322205635625129311769 (curve 346 stg2 B1=50000 sigma=980998724 thread=0)
01/04/26 10:14:19, prp25 = 9061920555519325508797997 (curve 316 stg2 B1=50000 sigma=8815958 thread=3)
01/04/26 10:14:35, prp25 = 9054322205635625129311769 (curve 668 stg2 B1=50000 sigma=3211061531 thread=1)
01/04/26 10:14:36, prp25 = 9061920555519325508797997 (curve 56 stg1 B1=50000 sigma=393137980 thread=1)
01/04/26 10:14:40, prp25 = 9054322205635625129311769 (curve 144 stg2 B1=50000 sigma=2363224082 thread=1)
01/04/26 10:14:57, prp25 = 9054322205635625129311769 (curve 722 stg2 B1=50000 sigma=4149143633 thread=0)
01/04/26 10:14:58, prp25 = 9054322205635625129311769 (curve 8 stg2 B1=50000 sigma=784134624 thread=0)
01/04/26 10:15:00, prp25 = 9061920555519325508797997 (curve 86 stg2 B1=50000 sigma=4097669478 thread=1)
01/04/26 10:15:03, prp25 = 9054322205635625129311769 (curve 144 stg1 B1=50000 sigma=3302536213 thread=0)
01/04/26 10:15:10, prp25 = 9054322205635625129311769 (curve 269 stg2 B1=50000 sigma=2482232394 thread=3)
01/04/26 10:15:10, prp25 = 9061920555519325508797997 (curve 11 stg2 B1=50000 sigma=3553703154 thread=2)
01/04/26 10:15:12, prp25 = 9061920555519325508797997 (curve 76 stg2 B1=50000 sigma=3955390889 thread=1)
01/04/26 10:15:13, prp25 = 9054322205635625129311769 (curve 31 stg2 B1=50000 sigma=1716497313 thread=1)
01/04/26 10:15:22, prp25 = 9061920555519325508797997 (curve 349 stg2 B1=50000 sigma=3969031017 thread=0)
01/04/26 10:15:22, prp25 = 9061920555519325508797997 (curve 2 stg2 B1=50000 sigma=861131006 thread=1)
01/04/26 10:15:25, prp25 = 9061920555519325508797997 (curve 111 stg2 B1=50000 sigma=1181642397 thread=2)
01/04/26 10:15:28, prp25 = 9054322205635625129311769 (curve 145 stg2 B1=50000 sigma=3309387316 thread=1)
01/04/26 10:15:30, prp25 = 9061920555519325508797997 (curve 83 stg2 B1=50000 sigma=606267993 thread=3)
01/04/26 10:15:31, prp25 = 9061920555519325508797997 (curve 29 stg2 B1=50000 sigma=3482158718 thread=0)
01/04/26 10:17:50, prp25 = 9054322205635625129311769 (curve 38 stg2 B1=50000 sigma=2326224346 thread=3)
01/04/26 10:18:06, prp25 = 9054322205635625129311769 (curve 639 stg2 B1=50000 sigma=2035465577 thread=1)
01/04/26 10:18:12, prp25 = 9061920555519325508797997 (curve 249 stg2 B1=50000 sigma=2088648328 thread=3)
01/04/26 10:18:13, prp25 = 9054322205635625129311769 (curve 60 stg2 B1=50000 sigma=1570210853 thread=0)
01/04/26 10:18:15, prp25 = 9054322205635625129311769 (curve 65 stg2 B1=50000 sigma=1871950522 thread=1)
01/04/26 10:18:16, prp25 = 9054322205635625129311769 (curve 43 stg2 B1=50000 sigma=335518488 thread=1)
01/04/26 10:18:16, prp25 = 9061920555519325508797997 (curve 5 stg2 B1=50000 sigma=662377729 thread=2)
01/04/26 10:18:17, prp25 = 9054322205635625129311769 (curve 9 stg2 B1=50000 sigma=4007694597 thread=3)
01/04/26 10:18:20, prp25 = 9061920555519325508797997 (curve 136 stg2 B1=50000 sigma=611188501 thread=2)
01/04/26 10:18:24, prp25 = 9054322205635625129311769 (curve 157 stg2 B1=50000 sigma=50954800 thread=1)
01/04/26 10:18:26, prp25 = 9054322205635625129311769 (curve 65 stg1 B1=50000 sigma=1814503551 thread=2)
01/04/26 10:18:28, prp25 = 9054322205635625129311769 (curve 77 stg2 B1=50000 sigma=221100989 thread=3)
01/04/26 10:18:30, prp25 = 9061920555519325508797997 (curve 109 stg2 B1=50000 sigma=3640644427 thread=1)
01/04/26 10:18:31, prp25 = 9054322205635625129311769 (curve 3 stg2 B1=50000 sigma=524123217 thread=0)
01/04/26 10:18:38, prp25 = 9061920555519325508797997 (curve 285 stg2 B1=50000 sigma=3357589224 thread=0)
01/04/26 10:18:40, prp25 = 9061920555519325508797997 (curve 69 stg2 B1=50000 sigma=541304158 thread=3)
01/04/26 10:18:40, prp25 = 9061920555519325508797997 (curve 5 stg2 B1=50000 sigma=1889004997 thread=1)
01/04/26 10:18:41, prp25 = 9061920555519325508797997 (curve 22 stg2 B1=50000 sigma=794473325 thread=2)
01/04/26 10:18:42, prp25 = 9061920555519325508797997 (curve 38 stg2 B1=50000 sigma=3021410276 thread=1)
01/04/26 10:18:43, prp25 = 9061920555519325508797997 (curve 71 stg2 B1=50000 sigma=76473112 thread=3)
01/04/26 10:18:48, prp25 = 9061920555519325508797997 (curve 196 stg2 B1=50000 sigma=3121013462 thread=3)
01/04/26 10:18:50, prp25 = 9054322205635625129311769 (curve 54 stg2 B1=50000 sigma=1507915467 thread=3)
01/04/26 10:18:50, prp25 = 9054322205635625129311769 (curve 19 stg2 B1=50000 sigma=1480976207 thread=2)
01/04/26 10:18:54, prp25 = 9054322205635625129311769 (curve 148 stg2 B1=50000 sigma=2565236678 thread=3)
01/04/26 10:18:54, prp25 = 9054322205635625129311769 (curve 3 stg2 B1=50000 sigma=4288533629 thread=3)
01/04/26 10:18:57, prp25 = 9061920555519325508797997 (curve 102 stg2 B1=50000 sigma=3994479613 thread=0)
01/04/26 10:19:00, prp25 = 9061920555519325508797997 (curve 152 stg2 B1=50000 sigma=2910431219 thread=3)
01/04/26 10:19:10, prp25 = 9054322205635625129311769 (curve 394 stg2 B1=50000 sigma=350540350 thread=3)
01/04/26 10:19:31, prp25 = 9054322205635625129311769 (curve 898 stg2 B1=50000 sigma=3910881346 thread=3)
01/04/26 10:19:34, prp25 = 9054322205635625129311769 (curve 101 stg2 B1=50000 sigma=1109269916 thread=2)
01/04/26 10:19:36, prp25 = 9054322205635625129311769 (curve 92 stg2 B1=50000 sigma=1858165063 thread=3)
01/04/26 10:19:38, prp25 = 9061920555519325508797997 (curve 67 stg2 B1=50000 sigma=2896897280 thread=0)
01/04/26 10:19:40, prp25 = 9061920555519325508797997 (curve 58 stg2 B1=50000 sigma=3302880242 thread=1)
01/04/26 10:19:44, prp25 = 9054322205635625129311769 (curve 152 stg2 B1=50000 sigma=63949271 thread=1)
01/04/26 10:19:45, prp25 = 9054322205635625129311769 (curve 51 stg2 B1=50000 sigma=2598491651 thread=2)
01/04/26 10:19:45, prp25 = 9061920555519325508797997 (curve 14 stg2 B1=50000 sigma=2780492 thread=0)
01/04/26 10:19:56, prp25 = 9061920555519325508797997 (curve 446 stg2 B1=50000 sigma=1259253095 thread=1)
01/04/26 10:19:57, prp25 = 9054322205635625129311769 (curve 11 stg2 B1=50000 sigma=237698144 thread=0)
01/04/26 10:20:05, prp25 = 9054322205635625129311769 (curve 353 stg2 B1=50000 sigma=4155787874 thread=1)
01/04/26 10:20:10, prp25 = 9054322205635625129311769 (curve 201 stg2 B1=50000 sigma=2784475232 thread=3)
01/04/26 10:20:12, prp25 = 9054322205635625129311769 (curve 96 stg2 B1=50000 sigma=3121268214 thread=0)
01/04/26 10:20:14, prp25 = 9061920555519325508797997 (curve 55 stg2 B1=50000 sigma=2912699549 thread=2)
01/04/26 10:20:17, prp25 = 9054322205635625129311769 (curve 117 stg2 B1=50000 sigma=2886770137 thread=2)
01/04/26 10:20:22, prp25 = 9061920555519325508797997 (curve 220 stg2 B1=50000 sigma=271310281 thread=2)
01/04/26 10:20:25, prp25 = 9061920555519325508797997 (curve 126 stg2 B1=50000 sigma=1256457860 thread=3)
01/04/26 10:20:33, prp25 = 9061920555519325508797997 (curve 307 stg2 B1=50000 sigma=4279760972 thread=3)
01/04/26 10:20:37, prp25 = 9054322205635625129311769 (curve 177 stg2 B1=50000 sigma=2587156057 thread=2)
01/04/26 10:20:40, prp25 = 9054322205635625129311769 (curve 130 stg2 B1=50000 sigma=1943282695 thread=0)
01/04/26 10:20:42, prp25 = 9061920555519325508797997 (curve 83 stg2 B1=50000 sigma=3639315186 thread=0)
01/04/26 10:20:43, prp25 = 9061920555519325508797997 (curve 8 stg2 B1=50000 sigma=2251671644 thread=0)
01/04/26 10:20:53, prp25 = 9061920555519325508797997 (curve 419 stg2 B1=50000 sigma=1698481221 thread=2)
01/04/26 10:21:03, prp25 = 9061920555519325508797997 (curve 405 stg1 B1=50000 sigma=3595928772 thread=3)
01/04/26 10:21:04, prp25 = 9061920555519325508797997 (curve 42 stg2 B1=50000 sigma=1150875487 thread=0)
01/04/26 10:21:06, prp25 = 9054322205635625129311769 (curve 105 stg2 B1=50000 sigma=157178765 thread=0)
01/04/26 10:21:08, prp25 = 9054322205635625129311769 (curve 59 stg2 B1=50000 sigma=3272633817 thread=0)
01/04/26 10:21:10, prp25 = 9054322205635625129311769 (curve 81 stg2 B1=50000 sigma=3152960343 thread=1)
01/04/26 10:21:11, prp25 = 9054322205635625129311769 (curve 34 stg2 B1=50000 sigma=668899445 thread=1)
01/04/26 10:21:11, prp25 = 9054322205635625129311769 (curve 5 stg2 B1=50000 sigma=3331028720 thread=3)
01/04/26 10:21:11, prp25 = 9054322205635625129311769 (curve 5 stg2 B1=50000 sigma=252425537 thread=3)
01/04/26 10:21:29, prp25 = 9061920555519325508797997 (curve 730 stg2 B1=50000 sigma=2596328889 thread=1)
01/04/26 10:21:31, prp25 = 9054322205635625129311769 (curve 78 stg2 B1=50000 sigma=2049298676 thread=2)
01/04/26 10:21:35, prp25 = 9054322205635625129311769 (curve 164 stg2 B1=50000 sigma=782367959 thread=3)
01/04/26 10:21:41, prp25 = 9061920555519325508797997 (curve 240 stg2 B1=50000 sigma=2649024263 thread=1)
01/04/26 10:21:42, prp25 = 9061920555519325508797997 (curve 25 stg2 B1=50000 sigma=1084680091 thread=3)
01/04/26 10:21:43, prp25 = 9061920555519325508797997 (curve 37 stg2 B1=50000 sigma=2318072585 thread=2)
01/04/26 10:21:47, prp25 = 9061920555519325508797997 (curve 154 stg2 B1=50000 sigma=3910102790 thread=3)
01/04/26 10:21:59, prp25 = 9054322205635625129311769 (curve 527 stg2 B1=50000 sigma=3435379260 thread=3)
01/04/26 10:22:00, prp25 = 9061920555519325508797997 (curve 33 stg2 B1=50000 sigma=2441263867 thread=3)
01/04/26 10:22:05, prp25 = 9061920555519325508797997 (curve 185 stg1 B1=50000 sigma=2127284938 thread=2)
01/04/26 10:22:06, prp25 = 9061920555519325508797997 (curve 14 stg2 B1=50000 sigma=3461271214 thread=2)
Я вижу что 23 раза из 100, или 23%, что почему то заметно меньше 37%. Заметьте, один раз понадобилось практически 900 кривых, 3 раза больше 700, 5 раз больше 600, 7 раз больше 428. PS. PS Это же очевидно. Но пока не получается проверить что будет программа делать в таком случае
Набирать статистику для разбирательства как работает программа на огромных числах (256 бит) и ждать каждый раз часы - ИМХО извращение, проще тестировать на меньших числах.
|

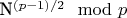
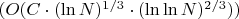
 ? при полиномах 2-й степени он значит
? при полиномах 2-й степени он значит  , а для всех остальных начиная с 3-й, становится
, а для всех остальных начиная с 3-й, становится 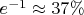 , но учитывая что проверяются ещё и все меньшие кривые, она заметно ниже. Но точно не нулевая, вот например несколько запусков на одном и том же числе:
, но учитывая что проверяются ещё и все меньшие кривые, она заметно ниже. Но точно не нулевая, вот например несколько запусков на одном и том же числе: