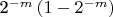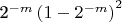==================== 'full' battery report ====================
Generator name: LCG64str2
Output size, bits: 64
Used seed: _05_IsL/FV/cOWaV95vA+m2b266p+I9YI820XM3V3JmCkY0=
# Test name xemp p Interpretation Thr#
-------------------------------------------------------------------------------
1 monobit_freq 0.238029 0.406 Ok 3
2 byte_freq 0.975213 0.298 Ok 1
3 word16_freq 0.713387 0.689 Ok 2
4 bspace64_1d 944 0.961 Ok 5
5 bspace32_1d 32734 0.573 Ok 3
6 bspace32_1d_high 32578 0.852 Ok 5
7 bspace32_2d 1012 0.345 Ok 4
8 bspace32_2d_high 1018 0.278 Ok 1
9 bspace21_3d 756 0.939 Ok 4
10 bspace21_3d_high 792 0.602 Ok 1
11 bspace16_4d 822 0.213 Ok 1
12 bspace16_4d_high 803 0.448 Ok 4
13 bspace8_8d 789 0.643 Ok 4
14 bspace8_8d_high 790 0.630 Ok 4
15 bspace4_8d_dec 3 0.567 Ok 3
16 bspace4_16d 770 0.852 Ok 2
17 bspace4_16d_high 810 0.353 Ok 3
18 collover20_2d 56926 0.362 Ok 5
19 collover20_2d_high 56865 0.461 Ok 1
20 collover13_3d 113810 0.353 Ok 2
21 collover13_3d_high 113526 0.679 Ok 3
22 collover8_5d 57217 0.058 Ok 5
23 collover8_5d_high 56801 0.568 Ok 1
24 collover5_8d 57207 0.063 Ok 2
25 collover5_8d_high 56977 0.286 Ok 2
26 gap_inv8 118.585 0.545 Ok 3
27 gap_inv512 3784.82 0.845 Ok 5
28 gap_inv1024 9624.71 0.052 Ok 1
29 gap16_count0 -0.3728 0.645 Ok 2
30 hamming_distr -2.28173 0.989 Ok 5
31 hamming_ot 0.372902 0.355 Ok 1
32 hamming_ot_low1 0.0701581 0.472 Ok 3
33 hamming_ot_low8 1.40721 0.080 Ok 4
34 hamming_ot_values 0.975345 0.165 Ok 4
35 hamming_ot_u128 0.704417 0.241 Ok 4
36 hamming_ot_u256 -0.823346 0.795 Ok 3
37 hamming_ot_u512 -0.580147 0.719 Ok 5
38 linearcomp_high 500000 0.667 Ok 2
39 linearcomp_mid 500001 0.667 Ok 2
40 linearcomp_low 500001 0.667 Ok 1
41 matrixrank_4096 1.15489 0.561 Ok 4
42 matrixrank_4096_low8 1.60204 0.449 Ok 5
43 matrixrank_8192 6.05528 0.048 Ok 2
44 matrixrank_8192_low8 2.25263 0.324 Ok 3
45 mod3 -1.37018 0.915 Ok 5
46 sumcollector 20.9904 0.860 Ok 2
-------------------------------------------------------------------------------
Passed: 46
Suspicious: 0
Failed: 0
Quality (0-4): 4.00 (good)
Elapsed time: 00:48:09
Used seed: _05_IsL/FV/cOWaV95vA+m2b266p+I9YI820XM3V3JmCkY0=

 , то есть длиной в
, то есть длиной в  цифр в десятичной записи.
цифр в десятичной записи. , я не представляю, что такого,
, я не представляю, что такого, 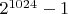 . Например, шифр Threefish-1024 в режиме гаммирования.
. Например, шифр Threefish-1024 в режиме гаммирования.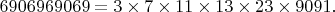
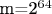 предложена Дж. Марсальей, у неё хорошие спектральные характеристики, и её легко запомнить. Вообще множители в LCG, запаздывания в генераторах Фибоначчи и сдвиги в LFSR без теоретического анализа трогать нельзя.
предложена Дж. Марсальей, у неё хорошие спектральные характеристики, и её легко запомнить. Вообще множители в LCG, запаздывания в генераторах Фибоначчи и сдвиги в LFSR без теоретического анализа трогать нельзя. на 56, то становится невероятно плохо на тесте который измеряет распределение расстояний между двумя одинаковыми байтами. Например, встретили в младшем байте число 42, сколько раз надо после этого выполнить генерацию следующего числа для того чтобы опять встретить 42?
на 56, то становится невероятно плохо на тесте который измеряет распределение расстояний между двумя одинаковыми байтами. Например, встретили в младшем байте число 42, сколько раз надо после этого выполнить генерацию следующего числа для того чтобы опять встретить 42? генераций описывается формулой:
генераций описывается формулой: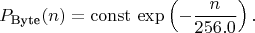
 почти не зависимо от значения повторяемого байта. А вот для этого алгоритма со сдвигом
почти не зависимо от значения повторяемого байта. А вот для этого алгоритма со сдвигом  -битов через
-битов через 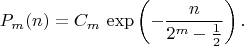 Почему там в знаменателе из
Почему там в знаменателе из  надо вычесть
надо вычесть  не знаю, удивительный экспериментальный факт. При больших
не знаю, удивительный экспериментальный факт. При больших  либо эта формула не верна, либо рандомные генераторы косячат. При увеличении числа испытаний оно к экспоненциальному хвосту что-то не сходится. Причём чем больше
либо эта формула не верна, либо рандомные генераторы косячат. При увеличении числа испытаний оно к экспоненциальному хвосту что-то не сходится. Причём чем больше 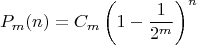 Надо было сначала подумать, а не подгонять под эксперимент
Надо было сначала подумать, а не подгонять под эксперимент  . Тогда вероятности выпадения интервалов длиной n будут такими:
. Тогда вероятности выпадения интервалов длиной n будут такими: