то что такого видит этот самый Birthday Spacings
Он делает следующее: берет выборку из m элементов (беззнаковых целых чисел, возвращаемых ГПСЧ), каждый из которых потенциально может принимать n значений. Нередко n равно
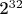
или
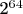
. Затем делается следующее:
1) Выборка сортируется по возрастанию, считается
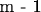
разностей соседних элементов в отсортированной выборке.
2)
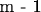
разностей снова сортируются по возрастанию.
3) В отсортированных разностях ищутся одинаковые значения. Число одинаковых пар значений приблизительно (асимптотически) подчиняется распределению Пуассона с
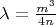
, обычно
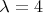
или 8. Для повышения чувствительности тест повторяют от десятков до тысяч раз, складывают ожидаемые значения и проверяют распределение суммы (другой вариант - сравнивают с распределением Пуассона по критерию хи-квадрат). Если p-значение выпадает из интервала
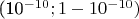
, то тест считается проваленным.
Работа с описанием теста:
https://doi.org/10.18637/jss.v007.i03У теста есть многомерные модификации, в которых значения набирают из старших или младших бит генератора. Их довольно много как в TestU01, так и в SmokeRand. Провал теста означает, что точки ложатся каким-то узором, обычно решетчатым. Тут дело в том, что Ваш скремблер основан на той же математике, что и сам LCG, т.е. умножениях и сложениях. И характерные для LCG решетки просто растягиваются и смещаются и, возможно, размываются, но не исчезают. В моем варианте я более активно использую "другую математику", т.е. побитовые операции и повороты.
Цитата:
И что конкретно означает "для научных расчётов он непригоден" если распределения фактически одинаковые?
Означает, что такая решетчатая структура может искажать какое-нибудь интегрирование или построение марковских цепей по Монте-Карло, оценку квантилей распределений по Монте-Карло и т.п. При систематическом провале теста Birthday Spacings проще не вдумываться, а сразу сказать "стоп, это игрушка", и выбросить генератор.
Цитата:
если распределения фактически одинаковые
Случайная равномерно распределенная последовательность подразумевает не только формальное соответствие равномерному распределению, но и несжимаемость (см. колмогоровскую сложность). Разумеется, вывод ГПСЧ имеет низкую колмогоровскую сложность, т.к. производится короткой программой. Но наилучший способ аппроксимировать высокую колмогоровскую сложность - это конструировать ГПСЧ так, чтобы человечеству не был известен способ сжать его вывод без полного перебора сидов, а сиды - достаточно длинны, чтобы это было бы затруднительно даже со сферой Дайсона. Такие ГПСЧ называются поточным шифрами. Остальное - полумеры.
P.S. Проходит ли Ваши тесты на моменты такой генератор:
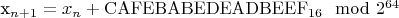
(т.н. Discrete Weyl Sequence)?