Одно допущение в СТО

[sergey zhukov]

Cos(x-pi/2)
Ну а если вот так. Забудем о физическом смысле всех величин, просто рассмотрим геометрическую задачу:

Я думаю, что ТС все правильно понимает. В смысле, что правильное понимание СТО у него есть, а эта вот идея - просто некоторое замечание. Трюк, как он сказал.

Конечно, от этого "трюка" нельзя требовать полной непротиворечивости, иначе это и было бы общепринятым представлением.

[realeugene]

sergey zhukov в сообщении #1711287 писал(а):

Я думаю, что ТС все правильно понимает. В смысле, что правильное понимание СТО у него есть, а эта вот идея - просто некоторое замечание.

У меня есть сомнения. А вот ваши уходы в оффтопик, мне кажется, мешают ему раскрыться.

[Cos(x-pi/2)]

sergey zhukov

sergey zhukov в сообщении #1711287 писал(а):

Забудем о физическом смысле всех величин, просто рассмотрим геометрическую задачу

Тогда эти ваши упражнения будут не для раздела "Физика" (причём, Вы ещё и делаете там грубую ошибку - на двух половинках рисунка обозначаете одинаковыми буквами разные по смыслу величины; это лучший способ запутаться самому или обмануть читателя.)

Ничего не могу сказать о понимании СТО у ТС, а вот понимаете ли Вы СТО - в этом я теперь сильно сомневаюсь. Ваши настойчивые попытки придать формулам СТО "евклидову" форму говорят мне о том, что Вы не понимаете глубокого физического смысла псевдоевклидовости геометрии Минковского в СТО.

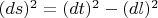
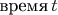
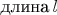
В СТО знак минус у одного из слагаемых в метрике Минковского $(ds)^2 = (dt)^2 - (dl)^2$ имеет очень важный физический смысл: этим знаком математически выражено фундаментальное различие между физическими понятиями $\text{время}\,t$ и $\text{длина}\,l$ (даже когда для измерения времени выбираются единицы длины). Хотя в популярной литературе пишут, что "СТО объединила понятия времени и пространства", но эти слова не означают исчезновения различия обоих понятий. СТО выявила их взаимосвязь, но не уничтожила их различие.

Это легко понять:

Из опыта известно, что в любой системе отсчёта время физически измеряется специальным прибором - часами (той или иной конструкции, конкретное устройство приборов не важно для этого рассуждения), а длины измеряются другим специальным прибором - некоторой линейкой. Физически приемлемое математическое описание принципа относительности (утверждающего, в частности, равноправие всех ИСО) должно гарантировать в правильной теории, что при переходе от одной ИСО к другой часы не превратятся в линейку, а линейка в часы. Подобное превращение означало бы ошибочность теории - ведь в экспериментах такого превращения нет.

"Гиперболические повороты" (которые Вам не нравятся и Вы с ними боретесь), т.е. преобразования Лоренца координат в пространстве-времени, описывающие в СТО переходы от одной ИСО к другой, как раз гарантируют различимость времён и длин. В СТО выражение для квадрата интервала с его сигнатурой (знаками плюс и минус) инвариантно:

$$(ds)^2 \,=\, (dt)^2 - (dl)^2\,=\, (dt')^2 - (dl')^2$$

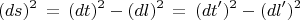
Инвариантны величины "собственных времён" (на времени-подобных мировых линиях - это тоже инвариантное понятие) и "собственных длин" (на пространственно-подобных линиях).

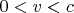
Наглядно на 2-мерных ПВ-диаграммах инвариантность различия между часами и линейками видна так: оси $t'$ и $x'$ ИСО', движущейся относительно неподвижной на данной диаграмме ИСО $(t,x),$ выглядят симметрично наклонёнными к образующей светового конуса, и тем сильнее, чем больше скорость $0<v<c$ движения систем отсчёта относительно друг друга, но эти оси не меняются местами, не переходят друг в друга.


На "аналогичной" же картине евклидовой плоскости с декартовыми координатами $y$ (вместо $t)$ и $x$ оси полностью равноправны, а метрика инвариантна при обычных поворотах осей:

$$(ds_E)^2=(dy)^2+(dx)^2=(dy')^2+(dx')^2$$

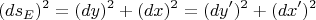
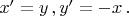
Взаимно перпендикулярные оси $(y,x)$ поворачиваются одинаково, превращаясь во взаимно перпендикулярные $y',x'.$ При повороте на $90°$ получаем $x'=y\,,y'=-x\,.$ То есть, при попытке интерпретации $y$ и $y'$ в роли времени $t$ и $t',$ в этом примере выходит, что в новой системе отсчёта часы должны совпасть с линейками, а линейки с часами, исходной системы отсчёта.

Можно привести ещё ряд примеров, из которых видно, что евклидова геометрия не подходит для пространства-времени. Например, возникает проблема с выводом волновых уравнений; а физика без волн - это не про наш мир, в полностью евклидовом мире получается не та физика, которую мы наблюдаем в опытах.

Ведь евклидова плоскость изотропна (это верно и для пространства с евклидовой геометрией любой размерности) - в отличие от плоскости с геометрией Минковского, где в каждой точке соприкасаются вершинами два световых конуса - "конус будущего" и "конус прошлого". Поэтому на евклидовой плоскости вообще нет обоснованного способа выбрать какое-либо направление в качестве оси времени какой-либо системы отсчёта.

То же самое другими словами: имеется различие в свойствах симметрии пространства с евклидовой геометрией и пространства с геометрией Минковского. Эти две различные симметрии описываются группой вращений и группой Лоренца, и обе группы отличаются друг от друга по своим свойствам. Для описания геометрии пространства-времени в физической теории оказалась подходящей именно группа Лоренца. А евклидова геометрия, хоть она и привычна со школьной скамьи, не подошла для описания геометрии пространства-времени.

На основе евклидовой геометрии нет способа физически разумно и столь же просто и естественно, как в геометрии Минковского, ввести в дело важнейшие понятия СТО, - световые конусы, времени- и пространственно-подобные линии, собственное время, собственная длина. И это ещё не весь перечень важных для физики понятий, адекватно описываемых математикой СТО, основанной именно на геометрии Минковского, а не евклидовой:

В физике важны законы преобразования не только пространственно-временных координат, но и соответствующие лоренц-преобразования всяких полевых величин: скалярных, спинорных, тензорных различного ранга - все они находят применение в задачах классической и квантовой теории поля. Фундаментальный физический принцип относительности проявляется как ковариантность (неизменность формы) полевых уравнений всех видов при преобразованиях Лоренца. Это один из основных критериев выбора теоретических моделей в физике элементарных частиц. Такой подход привёл ко многим теоретическим предсказаниям, затем успешно подтвердившимся в опытах. Этот факт служит одним из подтверждений СТО и правильности заложенной в основу СТО идеи о наличии геометрии Минковсого в пространстве-времени.


А желание придумывать трюки, чтобы только переписать одну формулу из СТО в другом виде, внешне похожем на вызубренную в школе теорему Пифагора, это что такое... Это ваше личное дело: хотите заниматься ерундой, притом на страницах форума, хорошо, не буду больше реагировать на подобные ваши изыскания. Занимайтесь этим, если модераторы не остановят. К серьёзной физике эта ваша детская игра не имеет отношения.

[sergey zhukov]

Cos(x-pi/2)
Ну конечно. Я уже давно все это забросил и, разумеется, не "борюсь" с псевдоевклидовой геометрией, гиперболическими поворотами, и не считаю время просто еще одной пространственной координатой, а пространство-время - изотропным.

Все это было в свое время, поэтому я сразу понял, что имеет ввиду ТС. И сразу сказал ему, что все это хотя и увлекательно, и никуда не ведет и по сути неправильно. Знак "минус" в формуле интервала невозможно обойти никакими трюками. Да он и сам это понимает, я думаю, поскольку говорит, что это "одно допущение" и "трюк", а вовсе не "вот как все на самом деле".

Я знаю, что многие стремятся понять СТО "с евклидовой" стороны, и часто кажется, что там действительно все складывается и становится понятнее. Но это только кажется.

Cos(x-pi/2) в сообщении #1711349 писал(а):

причём, Вы ещё и делаете там грубую ошибку - на двух половинках рисунка обозначаете одинаковыми буквами разные по смыслу величины

Это да. Но вот об этом речь изначально и была. Вот о таком рисунке с такими обозначениями. Я думаю, ТС согласится, что это он и имел в виду.

Еще раз для ясности скажу: я это представление не поддерживаю. Пространство-время нельзя непротиворечиво отобразить на евклидовой плоскости. Всякие заманчивые "трюки" - это просто игрушки.

[DimaM]

(Cos(x-pi/2))

Cos(x-pi/2) в сообщении #1711349 писал(а):

Из опыта известно, что в любой системе отсчёта время физически измеряется специальным прибором - часами (той или иной конструкции, конкретное устройство приборов не важно для этого рассуждения), а длины измеряются другим специальным прибором - некоторой линейкой.

Строго говоря, расстояния измеряются тоже часами (см. эталон метра).

[epros]

MC_Quadrat в сообщении #1711379 писал(а):

Каждый буст вдоль координаты x или y эквивалентен повороту 4-вектора на угол $\alpha$ в соответствующей плоскости (w,x) или (w,y), где
$\beta=v/c=\sin\alpha$

Что Вы хотели здесь нам открыть? Это общеизвестно, что если координату времени рассматривать как мнимую, то преобразование Лоренца можно записать как поворот на мнимый угол. См. статью Википедии про преобразование Лоренца.

[MC_Quadrat]

Cos(x-pi/2) в сообщении #1711099 писал(а):

К сожалению, ТС не отвечает на вопрос, как он из своих соображений получает формулы СТО (если действительно получает их), и какое преимущество дают его соображения перед стандартными. Без чётко обоснованных выкладок всё это словесное творчество выглядит путаницей, пригодной только для Пургатория. Хотя раздел форума здесь дискуссионный, но СТО - наука давно уже не дискуссионная. Не надо здесь пытаться её переиначивать непродуманной отсебятиной.

Извиняюсь, что долго не отвечал.
Я нигде не утверждал, что это физ теория/модель. Это дидактический прием-упрощение. Поэтому и обвинять в лженаучности меня не стоит. Все формулы и преобразования выводятся из начальных условий первого поста в любом текстовом ИИ.
Я хотел бы ответить на вопрос не как и что, а зачем.
Рассмотрим задачу СТО:
Даны три инерциальные системы A, B, C
Система B движется относительно A со скоростью $v_1=0.6c$ вдоль оси x.
Система C движется относительно B со скоростью $v_2=0.5c$ вдоль оси y.

Рассмотрим точечную частицу, которая покоится в системе C.

Найти (относительно системы A):
Компоненты скорости частицы $v_x$ и $v_y$ в долях от c;
Модуль её скорости v;
Фактор Лоренца $\gamma$ (время жизни / замедление времени) относительно A.

Решение.
Каждый буст вдоль координаты x или y эквивалентен повороту 4-вектора на угол $\alpha$ в соответствующей плоскости (w,x) или (w,y), где
$\beta=v/c=\sin\alpha=0.6$, $\gamma=1/\cos\alpha=1.25$ .
Сделаем 2 последовательных перпендикулярных поворота:
после первого поворота (угол $\alpha_1$ по x) и второго (угол $\alpha_2$ по y) компоненты 4-вектора становятся
$u_x=c\sin\alpha_1$,
$u_y=c\cos\alpha_1\sin\alpha_2$,
$u_w=c\cos\alpha_1\cos\alpha_2$​.
Наблюдаемая трёхмерная скорость равна просто $v_i=u_i$. Тогда
$v_x=c\sin\alpha_1=0.6c$,
$v_y=c\cos\alpha_1\sin\alpha_2=0.4c$,
а фактор Лоренца $\gamma=\frac{1}{\cos\alpha_1\cos\alpha_2}$=1.44
То есть всё выражается через элементарную тригонометрию — никакой матричной алгебры.

realeugene в сообщении #1711139 писал(а):

MC_Quadrat в сообщении #1710480 писал(а):

при $\alpha$=90 — свет, времени нет

А что тогда такое "скорость света"?

максимальная поперечная проекция полной мировой скорости.

epros в сообщении #1711408 писал(а):

MC_Quadrat в сообщении #1711379 писал(а):

Каждый буст вдоль координаты x или y эквивалентен повороту 4-вектора на угол $\alpha$ в соответствующей плоскости (w,x) или (w,y), где
$\beta=v/c=\sin\alpha$

Что Вы хотели здесь нам открыть? Это общеизвестно, что если координату времени рассматривать как мнимую, то преобразование Лоренца можно записать как поворот на мнимый угол. См. статью Википедии про преобразование Лоренца.

Я ж тут не диссертацию защищаю.
Пример приведенной задачи имеет отличие в том, что сложение скоростей происходит без тензоров, мнимых углов, рапидности, а как обычное сложение реальных углов.

Хотя в этой задаче и не использовались симметрии скорости и энергии. Если кого-то заинтересует, я могу привести решение задачи с использованием "закона сохранения энергии в 4d"(к законам нашей вселенной отношения не имеет), но придется подождать.

[MC_Quadrat]

DimaM в сообщении #1710548 писал(а):

MC_Quadrat
Какие-то из формул при этом получаются проще, чем в традиционной формулировке? Например, преобразования Лоренца как выводятся?

Примеры формул, которые получаются проще:
Лоренц-фактор
$\gamma=1/\cos\alpha$
$v=c\sin\alpha$
Замедление времени
$d\tau=dt\cos\alpha$
Сложение скоростей
$\alpha=\alpha_1+\alpha_2$
Вывод преобразований Лоренца:
Поворот $\begin{pmatrix} x' \\ w' \\ \end{pmatrix}$=$\begin{pmatrix} \cos\alpha -\sin\alpha \\ \sin\alpha \cos\alpha \\ \end{pmatrix}$\begin{pmatrix} x \\ w \\ \end{pmatrix}$$
и затем просто подставляем $w=ct$.
Энергия и импульс
$P=mU$
$U=(c\sin\alpha,c\cos\alpha)$.
Следовательно
$E=mc^2/\cos\alpha$
$p=mc\tg\alpha$
Энергетический баланс при распаде частицы
$\cos\alpha_i=m_i/M$

[Cos(x-pi/2)]

MC_Quadrat

MC_Quadrat в сообщении #1711435 писал(а):

Примеры формул, которые получаются проще:

Как бы они ни получались, сами эти формулы не проще - в них надо ещё выразить формальные углы через измеряемые в экспериментах скорости. И от этой простоты ничего не останется: всё вернётся к стандартной формулировке СТО, а она более проста в том смысле, что она обходится без таких формальных понятий, как не измеряемые непосредственно углы во вспомогательном евклидовом пространстве. (Ну, это лишь моё частное мнение; конечно, у разных людей могут быть разные представления о простоте в задачах физики.)

MC_Quadrat в сообщении #1711431 писал(а):

Все формулы и преобразования выводятся из начальных условий первого поста в любом текстовом ИИ.

ИИ на этом форуме не "авторитет", ссылаться на ИИ здесь не надо. Если можете сами что-то нужное для вашей аргументации обоснованно вывести, то выводите явно; или приводите точную ссылку на учебную или научную литературу по обсуждаемой Вами теме.

А задачка, которую Вы привели для примера, решается по общеизвестной формуле СТО для преобразования скоростей вообще сразу, без тригонометрии:

По условию задачки скорость частицы $\vec{v}$ относительно системы В равна известной скорости системы С относительно системы В, которая в свою очередь движется с известной скоростью $\vec{V}\perp \vec{v}$ относительно А. Поэтому скорость частицы $\vec{v}^{\,'}$ относительно А есть, согласно СТО,

$$\vec{v}^{\,'}=\frac{\vec{V}+\vec{v}_{||}+\vec{v}_{\perp}\sqrt{1-V^2}}{1+\vec{v}\cdot\vec{V}}=\vec{V}+\vec{v}_{\perp}\cdot 0.8$$

где значки $\,_{||}$ и $\,_{\perp}$ означают продольную и перпендикулярную части вектора $\vec{v}$ по отношению к $\vec{V}.$ Таким образом, ответ виден сразу: $v'_x=V=0.6\,,$ $v'_y=0.5\cdot 0.8=0.4\,.$ Два гамма-фактора перемножаются тоже безо всякой тригонометрии.

Если бы задачка была посложнее (например, с произвольными направлениями скоростей), то и в евклидовом варианте пришлось бы перемножать матрицы поворотов. Ну и вообще, такой евклидов формализм это тот общеизвестный формализм, о котором выше уже сказал epros.

Зачем Вы в своём стартовом сообщении упоминали какую-то "среду в 4-мерном евклидовом пространстве", и какое "допущение в СТО" подразумевается в названии темы - непонятно. СТО, как говорится, вся изъезжена вдоль и поперёк (до нас :).

(DimaM)

DimaM в сообщении #1711384 писал(а):

Строго говоря, расстояния измеряются тоже часами (см. эталон метра).

Строго говоря, нет.

Вот модельное (упрощённое) рассуждение и вопрос к Вам:

Допустим, Вы стоите на дороге. Ваши наручные часы показывают ваше собственное время. Допустим, ваша задача: разметить дорогу отметками, например, "1 км", "2 км", и т.д.

Вопрос: как Вы это сделаете с помощью только наручных часов?

Думаю, это невозможно, даже если вдоль дороги как-нибудь расположатся многочисленные ваши ассистенты с такими же часами.

Понятно же: чтобы воспользоваться определением метра, на которое Вы сослались, необходимы кроме часов ещё источник света, приёмник света и зеркало на подходящем расстоянии от источника света. Совокупность всех этих устройств, нужных для измерения расстояний, это уже другой прибор - "линейка".

[MC_Quadrat]

(Оффтоп)

Цитата:

Вот модельное (упрощённое) рассуждение и вопрос к Вам:

Допустим, Вы стоите на дороге. Ваши наручные часы показывают ваше собственное время. Допустим, ваша задача: разметить дорогу отметками, например, "1 км", "2 км", и т.д.

Вопрос: как Вы это сделаете с помощью только наручных часов?

Думаю, это невозможно, даже если вдоль дороги как-нибудь расположатся многочисленные ваши ассистенты с такими же часами.

Понятно же: чтобы воспользоваться определением метра, на которое Вы сослались, необходимы кроме часов ещё источник света, приёмник света и зеркало на подходящем расстоянии от источника света. Совокупность всех этих устройств, нужных для измерения расстояний, это уже другой прибор - "линейка".

Извините, вопрос адресован не мне, но как раз касается сути обсуждаемой темы и "каком-то одном допущении". Изложу свое ошибочное видение
Пусть:
вы (наблюдатель) стоите и на ваших часах проходит интервал t;
ваш ассистент бежит равномерно и за тот же «наблюдательный» отрезок показывает $t-\Delta t$ ;
предполагаем, что разница обусловлена чисто релятивистским кинетическим замедлением (не гравитацией и не дефектом хронометров).
Тогда ​$L=ct\cfrac{\sqrt{1-(1-\Delta t/t)^2}}{1-\Delta t/t}$ или $L=ct\tg\alpha$.
От скорости света c также можно избавиться при переходе к безразмерным единицам c.
Окончательно формула станет $L=\sqrt{t^2-(t-\Delta t)^2}$

[realeugene]

MC_Quadrat в сообщении #1710480 писал(а):

при $\alpha$=90 — свет, времени нет

На Луне установлен уголковый отражатель. В сторону Луны пуляют импульсом лазера и при помощи телескопа ловят момент, когда приходит отражение обратно. Рассчитайте время между импульсом лазера и приходом отражения обратно. Оно равно нулю?

[epros]

MC_Quadrat в сообщении #1711435 писал(а):

Сложение скоростей
$\alpha=\alpha_1+\alpha_2$

Что-то не сходится.

MC_Quadrat в сообщении #1711435 писал(а):

Вывод преобразований Лоренца:
Поворот $\begin{pmatrix} x' \\ w' \\ \end{pmatrix}$=$\begin{pmatrix} \cos\alpha -\sin\alpha \\ \sin\alpha \cos\alpha \\ \end{pmatrix}$\begin{pmatrix} x \\ w \\ \end{pmatrix}$$
и затем просто подставляем $w=ct$.

Этого не может быть, потому что в матрице преобразования Лоренца недиагональные члены имеют одинаковые знаки, а в матрице поворота - противоположные.

MC_Quadrat в сообщении #1711431 писал(а):

Пример приведенной задачи имеет отличие в том, что сложение скоростей происходит без тензоров, мнимых углов, рапидности, а как обычное сложение реальных углов.

Так что я что-то усомнился.

[realeugene]

MC_Quadrat в сообщении #1711431 писал(а):

Все формулы и преобразования выводятся из начальных условий первого поста в любом текстовом ИИ.

Ага: давно предлагаю за запощенный в форум бред ИИ наказывать как за собственный.

[Cos(x-pi/2)]

epros, матрица у ТС вроде правильная. Не вспомню, где (кроме имеющегося у меня своего старого рукописного конспекта) я впервые читал про этот формализм, но вот нашлась сейчвс на этой странице сайта eqworld книга 1962 года тётеньки Тоннелы - как раз с формулами преобразования Лоренца в разных вариантах; скриншоты:

(стандартная запись)

(с действительным углом)

(с мнимым углом)

MC_Quadrat

MC_Quadrat в сообщении #1711471 писал(а):

вы (наблюдатель) стоите и на ваших часах проходит интервал t;
ваш ассистент бежит равномерно и за тот же «наблюдательный» отрезок показывает $t-\Delta t$ ;

Чтобы вычислять расстояние между ними, они должны передавать друг другу сигналы с показаниями своих часов, т.е. нужны ещё специальные устройства. Как единое целое, наблюдатель плюс ассистент (с часами и с нужными приёмо-передающими устройствами) - это нелокальная, пространственно протяжённая система - это некоторая "линейка".

Напомню тот элементарный контекст, в котором я говорил, что $\text{часы}\,\neq\,\text{линейка}:$

(Оффтоп)

Часы у наблюдателя это локальный объект; говоря идеализированно, это материальная точка (со специальным внутренним устройством). Различные показания собственных часов наблюдателя изображаются на ПВ-диаграмме как точки (события) на мировой линии наблюдателя; в ИСО покоя наблюдателя можем представлять себе эту мировую линию как вертикальную прямую.

Совокупность столбиков с отметками расстояний вдоль дороги (ну или совокупность ассистентов с нужным оборудованием) изобразится на ПВ-диаграмме для фиксированного момента времени точками на горизонтальной прямой: это в данный момент "линейка" с отметками длины на ней.

На ПВ-диаграмме с другой ИСО мировая линия наблюдателя остаётся внутри светового конуса, а линейка - снаружи. С тем же результатом можно на прежней ПВ-диаграмме рассматривать другого, движущегося наблюдателя с его линейкой: мировая линия наблюдателя и его пространственно-подобная линейка всегда будут по разные стороны от образующей светового конуса, не совместятся друг с другом и не поменяются местами.

Это теоретическое утверждение означает с точки зрения экспериментатора, что локальные часы в кармане наблюдателя не превращаются в пространственно протяжённую систему, измеряющую длины (и наоборот: линейки не превращаются в часы).

В пространстве же с евклидовой геометрией нет времени, есть только расстояния. Световых конусов нет. Длины вдоль вертикальных линий измеряются вертикальной линейкой, а вдоль горизонтальных - горизонтальной линейкой. Поворачивай их как хочешь; легко одна встаёт на место другой.

Таково, на мой взгляд, возможное наглядное описание различия между группой Лоренца в ПВ и группой вращений в евклидовом пространстве на языке экспериментатора.

[realeugene]

Cos(x-pi/2) в сообщении #1711532 писал(а):

epros, матрица у ТС вроде правильная.

Сейчас очень опасно делать выводы про наличие у ТС какого-то понимания формализма просто по причине похожести некоторых написанных им формул на то, что встречалось когда-то в учебниках. ИИ позволяет вставлять в текст формулы любой сложности в качестве бреда без понимания сути.