Одно допущение в СТО

[MC_Quadrat]

Публикация статьи кватернионного пространства на Хабре датирована 2021 годом.

(Оффтоп)

И автор в этой теме "живет" уже минимум 5 лет. Поэтому пассажи о том, что ИИ ему нагенерил теорию явно характеризуют самих хохмачей.
Будьте аккуратнее в своем высокомерии, за ним может оказаться невежество.

Semenych в сообщении #1712105 писал(а):

Так что "велосипед" изобретен верно, он красивый, однако Льюис Эпштейн катается на нем уже лет 40
Рекомендую найти его книгу, вам понравится - там ваши мысли проиллюстрированы отличными картинками
ПРо галюны ИИ я вообще молчу, ChatGPT нахватался терминов из топологии и гидродинамики, смешал их в кашу и выдал вам "Униметрию"
Никакого физического смысла в "потоке кирпича", откалиброванном по функции Гудермана, нет и быть не может. Это словесная окрошка, нвукообразный бред

Если театр кукол с экраном был еще во времена Шекспира, это еще не значит, что не стоило изобретать телевизор.

[Buddha.Sugata]

sergey zhukov в сообщении #1712102 писал(а):

Автор, наверное, думает:
Интересно, а что такое "манифольд поверхности?". Ну ладно. Оставлю так. ИИ виднее. А вот "wick-ротация" и "мост на основе функции Гудермана" - это звучит! Это он хорошо ввернул! Стримлеты еще добавим для полной ясности.

я живу и работаю в немецко-англоязычной среде. Манифольд в прошлом для меня - арматура, манифольд в настоящем - многообразие, но часто этот термин встречается и в виде "манифольда" на русском. 3-manifold - это гиперповерхность трёхмерного тела в 4-ёхмерном пространсте:
https://en.wikipedia.org/wiki/3-manifold
Wick-rotation - известный и распространённый термин:
https://en.wikipedia.org/wiki/Wick_rotation
Функция Гудермана тоже известный мат. объект:
https://en.wikipedia.org/wiki/Gudermannian_function

Я назвал связь мостом. Стримлет - это маленький стрим. Ручеёк. Я такого зубоскальства с детского сада не встречал, когда объяснял детям, что ветер - причина, по которой качаются деревья. Не наоборот. Они использовали примерно похожий на Ваш приём защиты своего представления о мире.

-- 10.12.2025, 11:35 --

realeugene в сообщении #1712104 писал(а):

Buddha.Sugata
И для самого-самого начала, дайте, пожалуйста, определение кватернионного пространства, которое вы рассматриваете. Понятие пространства слишком перегружено, чтобы понимать его однозначно. Нужно строгое определение. Предположим, что такое кватернион я знаю.

Сперва вы просите на пальцах объяснить принцип, предполагая, вероятно, что "если ты не можешь на пальах объяснить ребёнку, чем занимаешься, то ты сам не знаешь, чем занимаешься", теперь, когда я объяснил на пальцах, вам не хватает математической формализации. Она есть в статье, которую вы отказываетесь читать, потому что она сложная. Какой смысл приводить это ещё раз здесь, если вы уже сказали, что этого не понимаете?

-- 10.12.2025, 11:41 --

Semenych в сообщении #1712105 писал(а):

Чтобы перейти от вашей красивой картинки к реальности, нужно делать поворот Вика ($t \to it$), и обычные синусы/косинусы превращаются в гиперболические ($\sinh, \cosh$)

Прежде, чем говорить о бреде давайте разберёмся в утверждениях, истинность которых можно проверить: то, о чём вы пишете - это Wick-преобразование. У меня преобразование через функцию Гудермана. Вы понимаете разницу?

-- 10.12.2025, 12:01 --

realeugene в сообщении #1712101 писал(а):

Buddha.Sugata в сообщении #1712077 писал(а):

Кирпичи в космосе подойдут. Каждый из кирпичей это поток.

Каждый? А в вакууме?

Допустим, есть один кирпич стандартных кирпичных размеров в виде куба со стороной один метр. Как выглядит его поток внутри и снаружи?

Какие плотность и состав у материала?

[MC_Quadrat]

(Оффтоп)

Buddha.Sugata в сообщении #1712114 писал(а):

sergey zhukov в сообщении #1712102 писал(а):

Я такого зубоскальства с детского сада не встречал

And people still laugh about as much as they ever did, despite their shrunken brains. If a bunch of them are lying around on a beach, and one of them farts, everybody else laughs and laughs, just as people would have done a million years ago

Buddha.Sugata
1. Как вы понимаете в униметрии энергию покоя? Насколько понимаю в фазовом пространстве то, что называется полной энергией =const?
2. Мне показалось, что в разрабатываемой вами модели уже прокинуты перспективные мостики к КМ?

[Buddha.Sugata]

MC_Quadrat в сообщении #1712116 писал(а):

[off]

Buddha.Sugata в сообщении #1712114 писал(а):

Buddha.Sugata
1. Как вы понимаете в униметрии энергию покоя? Насколько понимаю в фазовом пространстве то, что называется полной энергией =const?
2. Мне показалось, что в разрабатываемой вами модели уже прокинуты перспективные мостики к КМ?

1. Именно, в фазовом пространстве энергия покоя, то есть "количество потока" в собственной СК - инвариант, если нет структурных изменений потока.
2. К КМ просто заложена евклидовость пространства и $S^1$ топология стримлетов, дающие возможность воспроизвести (1) ненаблюдаемую глобальную фазу и (2) эффект неопределённости: фаза ненаблюдаема, потому что точки на стримлете неразличимы; неопределённость может возникать как следствие неопределённости в контакте двух стримлетов - измеряющего и измеряемого. Можно последнее представить как столкновение двух колец, при этом мы видим только их проекцию на одну наблюдаемую ось. Сложности начинаются на неравенствах Белла. У меня не хватает знаний в КМ, чтобы двигаться дальше в ту сторону.

[sergey zhukov]

Semenych в сообщении #1712105 писал(а):

Так что "велосипед" изобретен верно, он красивый

На дилетантском уровне наглядность ценится очень высоко. Даже часто это синоним правильности. Однако чем больше изучаешь разные научные представления, тем больше понимаешь, что "С какой стати там все должно быть наглядным? Это же просто везение, если так. А в общем случае наглядности никто не гарантирует. Она не обязана быть".

[realeugene]

MC_Quadrat в сообщении #1712109 писал(а):

И автор в этой теме "живет" уже минимум 5 лет.

Люди начали галюцинировать задолго до ИИ. ИИ сделал этот процесс эффективнее. На этот форум ранее приходили и очень образованные люди с очень качественным сильно математизированным бредом.

-- 10.12.2025, 12:25 --

Buddha.Sugata в сообщении #1712114 писал(а):

Какие плотность и состав у материала?

Да пусть будет обычная вода. Для ровного счёта - тонна на кубометр.

-- 10.12.2025, 12:30 --

Buddha.Sugata в сообщении #1712114 писал(а):

Она есть в статье, которую вы отказываетесь читать, потому что она сложная. Какой смысл приводить это ещё раз здесь, если вы уже сказали, что этого не понимаете?

А какой смысл писать на Хабре то, что я не понимаю?

От ваших статей возникает ощущение нагромождения. Они не просто сложны, но в них отсутствует опора на какой-то фундамент. Как и отсутствуют ссылки на базовую литературу. Этот фундамент я и прошу вас сейчас описать, шаг за шагом.

-- 10.12.2025, 12:52 --

sergey zhukov в сообщении #1712127 писал(а):

А в общем случае наглядности никто не гарантирует. Она не обязана быть

Наглядность - практически это синоним интуитивного понимания. В общем случае достижение интуитивного понимания требует много труда самого человека по осмыслению формальных построений.

[sergey zhukov]

realeugene
Ну да. Эта вот интуиция, натренированная на одном, вообще не обязана подходить под что-то другое. А нам кажется, что обязана.

Хорошо, конечно, когда удается "засунуть" новое в старую упаковку. Только не нужно думать, что это и есть самый правильный способ понимания всего нового и что это всегда должно быть возможно.

[realeugene]

Buddha.Sugata
С самого начала по новой статье:

Цитата:

Let (E, ⟨·, ·⟩) be a Euclidean proto–space

Существует множество различных структур, неформально называемых "евклидовым пространством". См. https://ru.wikipedia.org/wiki/%D0%95%D0 ... 0%B2%D0%BE Вы же на этом шаге не указываете даже размерность своего "протопространства". Три ли четыре?

-- 10.12.2025, 13:44 --

sergey zhukov
Кстати, "Relativity Visualized" похоже на самом деле хороша. Исторические экскурсы в её начале - так точно.
Арцюковский со своей "эфиродинамикой", оказывается, просто передирал до-СТОшную теорию лорда Кельвина.

[sergey zhukov]

realeugene
А я тоже все хотел ее прочесть, да как-то забывал. Книжка хорошая.

[Buddha.Sugata]

realeugene в сообщении #1712136 писал(а):

Существует множество различных структур, неформально называемых "евклидовым пространством". См. https://ru.wikipedia.org/wiki/%D0%95%D0 ... 0%B2%D0%BE Вы же на этом шаге не указываете даже размерность своего "протопространства". Три ли четыре?

Не менее 4. Там далее есть ремарка в таблице определений:

Цитата:

With these definitions, the observable space S is a 3-manifold embedded in a (minimum) 4-dimensional flow manifold S ⊕ span{et}.

кроме того из разложения:

Цитата:

Fix an observer’s orthonormal spatial triad {e1, e2, e3} ⊂ E and let S = span{e1, e2, e3} with orthogonal projectors PS and PS⊥.

нельзя выделить ничего ортогонального для $dim < 4$.
В объединении электрослабого и ЭМ взаимодействий вроде как используется вторая степень свободы во "времени", то есть возможно потребуется ещё одна ось, поэтому я не пишу 4 или 5. Для моделирования СТО достаточно 4.

realeugene в сообщении #1712129 писал(а):

От ваших статей возникает ощущение нагромождения. Они не просто сложны, но в них отсутствует опора на какой-то фундамент. Как и отсутствуют ссылки на базовую литературу. Этот фундамент я и прошу вас сейчас описать, шаг за шагом.

Ок. Понятно. Спасибо.

Мы задаём плоское 4-мерное евклидово пространство и вводим на нём элемент типа "движущаяся окружность" (постоянно вращающаяся "в себя"), который будем называть "стримлет". Абсолютно упругий при взаимодействиях в рассматриваемом пределе.
Можно это формализовать как поле скалярной фазы в каждой точке 4-пространства (при условии устранения многозначности фазы).
Далее мы должны ввести триплет пространственных ортов наблюдателя, чтобы получить разложение по ним проекции стримлета, у которого всегда будет одна общая ось с пространственным фреймом наблюдателя, а ненаблюдаемую часть такой проекции будем считать его "временем".
Введение кватернионнозначной функции на этом пространстве удобно тем, что мы можем сопоставить видимый 3-фрейм наблюдателя мнимому подпространству кватернионов, тогда время будет вещественным компонентом, и далее пользуясь лишь кватернионной алгеброй произвольно изменять этот 3-фрейм, моделируя различные системы отсчёта. Однако, трансляции должны выполняться как в исходном плоском евклидовом пространстве.

realeugene в сообщении #1712129 писал(а):

Да пусть будет обычная вода. Для ровного счёта - тонна на кубометр.

Вода в виде куба в вакууме?

[realeugene]

Buddha.Sugata в сообщении #1712156 писал(а):

Там далее есть ремарка

Мне совершенно не хочется додумывать базовую информацию из ремарок.

Buddha.Sugata в сообщении #1712156 писал(а):

Вода в виде куба в вакууме?

Какая вообще разница для этой теории? Если вам не нравится вода в виде куба в вакууме - возьмите идеальный куб из стали 45. Или из золота. Или выберите по своему желанию.

Buddha.Sugata в сообщении #1712156 писал(а):

Для моделирования СТО достаточно 4.

Замечательно. Ограничимся СТО. Значит, $R^4$ с евклидовым скалярным произведением?

Buddha.Sugata в сообщении #1712156 писал(а):

Абсолютно упругий при взаимодействиях в рассматриваемом пределе.

Эту фразу пока пропускаем: пока что у нас в фундаменте чистая геометрия без времени и, соответственно, какой-либо динамики.

Buddha.Sugata в сообщении #1712156 писал(а):

и вводим на нём элемент типа "движущаяся окружность" (постоянно вращающаяся "в себя")

В каком смысле "вращающаяся"? Времени пока что нет. Все 4 координаты - равноправные геометрические оси, больше никаких параметров нет. У 2-окружности в евклидовом 4-пространстве есть центр, радиус и 2-плоскость, в которой она лежит. Ортогональная к 2-плоскости другая 2-плоскость.

Buddha.Sugata в сообщении #1712156 писал(а):

у которого всегда будет одна общая ось с пространственным фреймом наблюдателя, а ненаблюдаемую часть такой проекции будем считать его "временем".

Выглядит как то, что мы выделяем трёхмерное линейное подпространство в нашем 4-мерном евклидовом пространстве, и ортогональную к этому подпространству ось называем осью времени. Верно?

Пока что можно остановиться.

-- 10.12.2025, 17:18 --

Buddha.Sugata

Цитата:

We introduce a phase potential as a real function

У вас нет условий дифференцируемости или даже непрерывности этой функции?

"Defect set $\Sigma$" - это конечное множество точек, или что-то другое?

[Buddha.Sugata]

realeugene в сообщении #1712160 писал(а):

Какая вообще разница для этой теории? Если вам не нравится вода в виде куба в вакууме - возьмите идеальный куб из стали 45. Или из золота. Или выберите по своему желанию.

Хорошо, пусть будет из золота. И вы правы - никакой разницы для этой теории нет

realeugene в сообщении #1712160 писал(а):

Замечательно. Ограничимся СТО. Значит, $R^4$ с евклидовым скалярным произведением?

Всё верно. $R^4$ с евклидовым скалярными произведением.

Цитата:

В каком смысле "вращающаяся"? Времени пока что нет. Все 4 координаты - равноправные геометрические оси, больше никаких параметров нет. У 2-окружности в евклидовом 4-пространстве есть центр, радиус и 2-плоскость, в которой она лежит. Ортогональная к 2-плоскости другая 2-плоскость.

В смысле, изменение фазы происходит постоянно. Времени наблюдателя ещё нет, если угодно. Абсолютное время не существует как абсолютное, в том смысле, что любое время - лишь калибр. Изменение фазы "по самой себе" в системе покоя даёт собственное время элементарных объектов. Хотя если рассматривать временной срез как в КМ, то, конечно, можно считать стримлет неподвижным. И если следовать логике "время из фазы" до конца, то в этом застывшем состоянии у фазового потока есть потенциал движения - та самая одноформа $\alpha = d\Phi$.
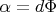
Касательно равноправности осей: в математическом смысле да, в физическом смысле - нет. Наблюдаемое 3-многообразие физически особенно, как минимум в том смысле, что геометрически условные 2-окружности наблюдаемых стримлетов его касаются или пересекают, как максимум - у него есть определённые свойства, e.g., диэлектрическая и магнитная проницаемость. Остальное верно.

realeugene в сообщении #1712160 писал(а):

Выглядит как то, что мы выделяем трёхмерное линейное подпространство в нашем 4-мерном евклидовом пространстве, и ортогональную к этому подпространству ось называем осью времени. Верно?

Верно.

realeugene в сообщении #1712160 писал(а):

У вас нет условий дифференцируемости или даже непрерывности этой функции?

1-форма требует её дифференцируемости и непрерывности как минимум на самой петле. Тут до сих пор существует вилка: считать петлю компактной (пространство тогда можно ужать до размерности 3) или оставить пространственной. Также открыт вопрос по дифференцируемости только вдоль петли или по всему $\mathcal E$, но ввиду того, что можно сперва взять дифференциал по петле в точке пересечения с наблдаемым пространством, а потом уже его вектор проецировать на пространство-"время", формулировки кажутся эквивалентными. Буду рад любой помощи и пояснениям в этом вопросе.

realeugene в сообщении #1712160 писал(а):

"Defect set $\Sigma$" - это конечное множество точек, или что-то другое?

Это конечное множество дефектов без уточнения геометрической формы последних, потому что если пойти по этому пути дальше, то потребуется минимум двухмерный дефект для существования вихря в 4д, и статья из переформулировки СТО превратиться в статью по топологии. Мой ответ - я пока не знаю. Можно предположить, что он несёт "самодефект" или наблюдаемое пространство само является дефектом, в котором фаза многозначна - ненаблюдаема, а ковектор брать в точке центра "обвивания". В любом случае спектр возможных вариантов позволяет сперва построить модель для СТО и, возможно, далее, так чтобы она согласовалась с эмпирикой, и по мере её построения собирать подсказки о требуемой топологии.

[realeugene]

Buddha.Sugata в сообщении #1712192 писал(а):

лишь калибр

Может быть вы лучше будете писать английскую терминологию? Применимый в данном контексте такой русский термин мне не известен.

-- 10.12.2025, 21:50 --

Buddha.Sugata в сообщении #1712192 писал(а):

Изменение фазы "по самой себе"

Что такое "изменение фазы само по себе"? У вас евклидово пространство $R^4$, как вы написали. Нет в математике времени. Вообще нет. В физике время - явный параметр, от которого зависит всё остальное.

-- 10.12.2025, 21:54 --

Buddha.Sugata в сообщении #1712192 писал(а):

Это конечное множество дефектов без уточнения геометрической формы последних

В соответствии с написанным в вашей статье выражением это множество точек - оно подмножество $R^4$. Множество точек или множество непонятно чего? Множество непонятно чего не может быть подмножеством $R^4$.

Ваша статья не проходит проверку формальной корректности простейших математических выражений из теории множеств в ней.

В общем, у меня на данный момент сложилось впечатление, что вы лишь жонглируете терминами, которые не понимаете. Даже судя по первым нескольким обсуждённым с вами предложениям. ИИ вам в этом жонглировании помогает жонглировать, но смысл не вносит.

[MC_Quadrat]

(Оффтоп)

Buddha.Sugata
Форумная публика представлет своего рода святую инквизицию. Никто из них не затруднит себя вникнуть в "статейку" на хабре, когда есть библии и прочие пыльные фоллианты. Здесь найдут запятую, через которую не только разрушат все, что вы создавали годами, просто на потеху зрителей, но и в вас посеят семя сомнений.
Поэтому я предлагаю зайти сразу с козырей. Иначе их под шконки не загнать. Ваша модель имеет неоспоримые преимущества в виде новых симметрий. Я бы попробовал найти классическую задачу СТО, решающуюся в сто действий и решить ее в 10. Здесь им уже нечем будет крыть.

[realeugene]

MC_Quadrat в сообщении #1712199 писал(а):

Форумная публика представлет своего рода святую инквизицию.

Форумная публика уже видела тут множество разного уровня альтов, думающих, что они годами совершают великое открытие, но на самом деле грубо не понимающих основ математики или физики.

В общем, вся тема уровня Пургатория. Что исходная идея ТС, что великое открытие, опубликованное на Хабре. Единственная польза - ссылка на книжку.