Дилетантские вопросы по линейной алгебре

[sydorov]

Уважаемый Anton_Peplov,

Попробую оттолкнуться от понятия тривиальности линейной комбинации

$\alpha \vec a + \beta \vec b + \gamma \vec c = \vec 0, когда \alpha = \beta = \gamma = 0.$

Выразим $\vec a$ через векторы базиса.

$\vec a = \alpha \vec a + \beta \vec b + \gamma \vec c$ - здесь ЛК $\alpha \vec a + \beta \vec b + \gamma \vec c$ - нетривиальная. И разложение по базису единственно.

$\vec a - \alpha \vec a = \beta \vec b + \gamma \vec c$

$(1 - \alpha) \vec a = \beta \vec b + \gamma \vec c$

$(1 - \alpha) \vec a - \beta \vec b - \gamma \vec c = \vec 0$ - здесь ЛК - уже тривиальная, т. е. $ (1 - \alpha) = - \beta = - \gamma = 0$

Получаем, что в разложении коэффициент $\alpha = 1$, а $\beta$ и $\gamma$ - нулевые. $\vec a = (1, 0, 0)$
Аналогично рассуждаем для $\vec b$ и $\vec c$

Простите, затупил. Продолжаю.

$f_4 (x, y, z) = x f_4 (1, 0, 0) + y f_4 (0, 1, 0) + z f_4 (0, 0, 1) = x (\alpha, 0, 0) + y (0, 1, 0) + z (0, 0, 1) = (\alpha x, 0, 0) + (0, y, 0) + (0, 0, z) = (\alpha x, y, z).$
Красоты не понимаю. Подскажите, плиз, "смысл анекдота" ) Ведь получено именно то, что в Вашем условии.

Anton_Peplov в сообщении #1709261 писал(а):

Если уж Вы так хотите наглядную аналогию, то вообразите - ну, не два трехмерных координатных пространства, это сложно, а просто две плоскости. Вспомните мою аналогию с двумя базисами и берите первый базис в одной плоскости, а второй - в другой. Вот Вам и будет изоморфизм между двумя плоскостями, т.е. между двумерными линейными пространствами.

Шикарная аналогия! А я не додумался. Это сообщение еще прорабатываю. Могу перенести его "в фон", если считаете нужным, и продолжить разбираться с линейными операторами.


Уважаемый svv, Ваше рассуждение

svv в сообщении #1709651 писал(а):

1) Пусть линейное отображение $f: V\to V$ не инъективно. Тогда существует вектор $v$, который является образом более чем одного вектора (назовём такой вектор амбициозным). То есть существуют такие $a$ и $b$, причём $a\ne b$, что
$f(a)=v$
$f(b)=v$
Пользуясь линейностью, находим разность:
$f(a-b)=0$, или
$f(c)=0$, где $c=a-b\ne 0$.
Из линейности также следует $f(0)=0$, поэтому $\operatorname{Ker}f$ содержит по крайней мере два вектора, $0$ и $c$.
Выходит, если некоторый вектор $v$ амбициозный, то и нулевой вектор тоже амбициозный.

Если же $\operatorname{Ker}f=\{0\}$, т.е. нулевой вектор неамбициозный, то всякий вектор неамбициозный, и отображение $f$ инъективно.

очень строгое, понятное, но я самостоятельно так бы не смог. Рассуждал нагляднее. А вот это определение: "Отображение $f: X\to Y$ биективно, если прообраз каждого элемента $y\in Y$ содержит ровно один элемент." вообще поразило меня минималистичностью. Сначала показалось, что его стоит дополнить следующим образом: прообраз каждого элемента $y\in Y$ содержит ровно один, принадлежащий только ему, элемент. Порассуждал, понял, что мое дополнение лишнее, и прозрел. Спасибо!

Господа, стоит ли мне подглядывать сейчас в какой-либо литературный источник?
До начала этой темы в качестве справочника использовал Ильина-Позняка, но сейчас мне он кажется немного "бедным".

[svv]

sydorov, и Вам спасибо. Перейдём к вопросу 2).

Итак, пусть $f: V\to V$ — линейное отображение и $\operatorname{ker}f=\{0\}$.
Мы выяснили, что тогда $f$ инъективно, иначе было бы $f(a)=f(b)$ для некоторых различных $a, b$, и тогда $f(c)=0$, где $c=a-b\neq 0$, то есть $c\in\operatorname{ker}f$, что противоречит условию.

Но, вроде бы, этого недостаточно, чтобы $f$ было сюръекцией? В самом деле, вдруг полный прообраз некоторого вектора пуст? Оказывается, всё же достаточно.

Пусть $\dim V=n$. Это значит, в $V$ существует базис из $n$ векторов, обозначим их $e_1,\ldots, e_n$, или кратко $(e_i)$. Обозначим их образы при отображении $f$ через $g_1, \ldots, g_n$:
$f(e_i)=g_i, \quad i=1,\ldots,n$
Вопрос: набор векторов $(g_i)$ линейно зависим (ЛЗ) или линейно независим (ЛН)?

Допустим, $(g_i)$ ЛЗ. Тогда существует нетривиальная линейная комбинация (в которой не все коэффициенты нулевые)
$\lambda_1 g_1+\ldots+\lambda_n g_n=0$
Пусть $a=\lambda_1 e_1+\ldots+\lambda_n e_n$. Поскольку $(e_i)$ — базис, он ЛН, поэтому $a\neq 0$. Тогда в силу линейности $f$
$f(a)=f(\lambda_1 e_1+\ldots+\lambda_n e_n)=\lambda_1 f(e_1)+\ldots+\lambda_n f(e_n)=\lambda_1 g_1+\ldots+\lambda_n g_n=0$
Но это означает, что ненулевой вектор $a\in\operatorname{ker}f$, что противоречит условию.

Значит, набор $(g_i)$ ЛН. Тогда он тоже базис. Тогда он полон, то есть любой вектор $v\in V$ представляется в виде
$v = \mu_1 g_1+\ldots+\mu_n g_n$
Тогда $v = f(b)$, где
$b = \mu_1 e_1+\ldots+\mu_n e_n$
То есть полный прообраз любого вектора $v$ непуст i.e. любой вектор лежит в образе $f$ i.e. $\operatorname{im} f = V$.

[Anton_Peplov]

sydorov в сообщении #1709727 писал(а):

Попробую оттолкнуться от понятия тривиальности линейной комбинации <...> Получаем, что в разложении коэффициент $\alpha = 1$, а $\beta$ и $\gamma$ - нулевые. $\vec a = (1, 0, 0)$

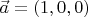
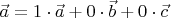
Вы все сделали правильно и строго, но длинновато. И без формальных манипуляций очевидно, что $\vec a = 1 \cdot \vec a + 0 \cdot \vec b + 0 \cdot \vec c$ является разложением вектора $\vec a$ по базису $\vec a, \vec b, \vec c$. Остается вспомнить, что разложение по базису единственно. Ну, это не беда, со временем научитесь видеть такие вещи с одного взгляда.

sydorov в сообщении #1709727 писал(а):

Красоты не понимаю. Подскажите, плиз, "смысл анекдота" ) Ведь получено именно то, что в Вашем условии.

Возможно, особой красоты и нет, это дело вкуса :) Я как раз хотел сказать, что из Ваших манипуляций получается именно то, что в условии. Раз Вы за них взялись, значит, еще не до конца освоились с координатами и векторами. Иначе бы сразу бы это увидели. Но вывод сделали правильный:

sydorov в сообщении #1709648 писал(а):

Базис $f_4(1, 0, 0), f_4(0, 1, 0), f_4(0, 0, 1): (\alpha, 0, 0), (0, 1, 0), (0, 0, 1).$

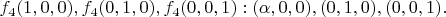
Только запишите векторы $(\alpha, 0, 0), (0, 1, 0), (0, 0, 1)$ не как набор координат (подсказка: они очевидным образом связаны с $\vec i, \vec j, \vec k$).

sydorov в сообщении #1709727 писал(а):

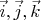
Господа, стоит ли мне подглядывать сейчас в какой-либо литературный источник?
До начала этой темы в качестве справочника использовал Ильина-Позняка, но сейчас мне он кажется немного "бедным".

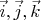
По результатам Ваших упражнений я делаю такой вывод. Вам знакомы основные теоремы, и кое-что Вы умеете доказывать сами. Но в некоторых вещах, которые должны быть ясны как дважды два и делаться в уме, Вы еще не тверды. Например, в понимании того факта, что координаты $(x, y, z)$ есть коэффициенты разложения по базису $\vec i, \vec j, \vec k$. Вам приходится вспоминать теоремы и проделывать вычисления.

Исходя из этого, я делаю вывод, что Вам нужен не учебник, а задачник. И не на доказательства, а на выполнение рутинных операций типа разложения заданного вектора по заданному базису. Может быть, задачник даже не по линейной алгебре, а по аналитической геометрии в той ее части, где проходят векторы. Не обязательно решать все задачи, которые есть в задачнике, их слишком много. Надо их решать, пока решать их не станет легко. Можно по одной-две в день. Набейте руку. Понимаю, это может быть скучным. Мне самому это всегда было скучно. Но без технических навыков не бывает настоящего понимания математики.

sydorov в сообщении #1709727 писал(а):

Могу перенести его "в фон", если считаете нужным, и продолжить разбираться с линейными операторами.

Отсутствие принципиальной разницы между изоморфизмом и автоморфизмом и то, что изоморфные линейные пространства в некотором смысле одно и то же пространство, стоит понять. А примеры изоморфизмов из других областей математики можно забыть. Все равно они пока Вам ничего не говорят. Если будете изучать эти области математики, тогда и увидите аналогию.

С линейными операторами осталось разбираться всего ничего, потому что произвольный линейный оператор устроен не намного сложнее изоморфизма. Чуть позже я раскрою эту тему подробнее.

[sydorov]

Уважаемый Anton_Peplov

Anton_Peplov в сообщении #1709261 писал(а):

1) покажите, что $(\mathbb R, 0)$ и $(0, \mathbb R)$ - это подпространства линейного пространства $\mathbb R^2$
2) постройте изоморфизм между $(\mathbb R, 0)$ и $(0, \mathbb R)$
3) постройте изоморфизм между $(\mathbb R, 0)$ и $\mathbb R$, а также между $(0, \mathbb R)$ и $\mathbb R$.

1) Подпрстранства понятны, каждое состоит из векторов коллинеарных соответствующему базисному вектору.
$(\mathbb R, 0)$
$\vec 0 \in \mathbb R$ и $\vec 0 \in \mathbb R^2.$ Не расписываю покоординатно.
$(x_1, 0) + (x_2, 0) = (x_1 + x_2, 0) \in (\mathbb R, 0)$
$\forall \alpha \in \mathbb R$
$\alpha (x, 0) = (\alpha x, 0) \in (\mathbb R, 0)$
Аналогично для $(0, \mathbb R)$

2) Делаем поворот
$f((x, 0)) = (0, x)$

3) Проецируем
$f_1((x, 0)) = f_2((0, x)) = x$

С дальнейшим Вашим объяснением оказалось не так уж и сложно, как показалось с первого раза. Спасибо. Прошу прощения, что медленно разбираюсь.

(Оффтоп)

Мой конек не скорость, а выносливость. В прошлом бегун на сверхдлинные )

Anton_Peplov в сообщении #1709832 писал(а):

Только запишите векторы $(\alpha, 0, 0), (0, 1, 0), (0, 0, 1)$ не как набор координат

Базис $$f_4(1, 0, 0), f_4(0, 1, 0), f_4(0, 0, 1): \alpha \vec i, \vec j, \vec k$

Anton_Peplov в сообщении #1709832 писал(а):

в некоторых вещах, которые должны быть ясны как дважды два и делаться в уме, Вы еще не тверды

Благодарю за такой эвфемизм ) Действительно, не набил руку, и в упражнениях по аналитической геометрии векторную технику почти не применял.
Последую Вашей рекомендации обратиться к задачнику. Имею под редакцией Смирнова. Вроде в нем достаточно задач по векторам на "найти" и "вычислить". Потренируюсь.

[sydorov]

Уважаемый svv,

svv в сообщении #1709269 писал(а):

2) Почему не надо проверять, что у любого вектора прообраз непуст?

svv в сообщении #1709789 писал(а):

Перейдём к вопросу 2).

Итак, пусть $f: V\to V$ — линейное отображение и $\operatorname{ker}f=\{0\}$.
Мы выяснили, что тогда $f$ инъективно, иначе было бы $f(a)=f(b)$ для некоторых различных $a, b$, и тогда $f(c)=0$, где $c=a-b\neq 0$, то есть $c\in\operatorname{ker}f$, что противоречит условию.

Но, вроде бы, этого недостаточно, чтобы $f$ было сюръекцией? В самом деле, вдруг полный прообраз некоторого вектора пуст? Оказывается, всё же достаточно.

Пусть $\dim V=n$. Это значит, в $V$ существует базис из $n$ векторов, обозначим их $e_1,\ldots, e_n$, или кратко $(e_i)$. Обозначим их образы при отображении $f$ через $g_1, \ldots, g_n$:
$f(e_i)=g_i, \quad i=1,\ldots,n$
Вопрос: набор векторов $(g_i)$ линейно зависим (ЛЗ) или линейно независим (ЛН)?

Допустим, $(g_i)$ ЛЗ. Тогда существует нетривиальная линейная комбинация (в которой не все коэффициенты нулевые)
$\lambda_1 g_1+\ldots+\lambda_n g_n=0$
Пусть $a=\lambda_1 e_1+\ldots+\lambda_n e_n$. Поскольку $(e_i)$ — базис, он ЛН, поэтому $a\neq 0$. Тогда в силу линейности $f$
$f(a)=f(\lambda_1 e_1+\ldots+\lambda_n e_n)=\lambda_1 f(e_1)+\ldots+\lambda_n f(e_n)=\lambda_1 g_1+\ldots+\lambda_n g_n=0$
Но это означает, что ненулевой вектор $a\in\operatorname{ker}f$, что противоречит условию.

Значит, набор $(g_i)$ ЛН. Тогда он тоже базис. Тогда он полон, то есть любой вектор $v\in V$ представляется в виде
$v = \mu_1 g_1+\ldots+\mu_n g_n$
Тогда $v = f(b)$, где
$b = \mu_1 e_1+\ldots+\mu_n e_n$
То есть полный прообраз любого вектора $v$ непуст i.e. любой вектор лежит в образе $f$ i.e. $\operatorname{im} f = V$.

Я очень внимательно проследил за ходом Вашего доказательства, чтобы для себя окончательно расставить точки над i в этом вопросе. Разобрался.
Теперь имею образец для подражания (которого мне если не достичь, то, во всяком случае, к которому стремиться), как необходимо рассуждать.
Огромное спасибо!

[svv]

sydorov, спасибо, очень приятно. Но вообще математическая строгость — это не по моей части, яжфизик.

[sydorov]

Уважаемый svv,

Ну, не скажите )

(Оффтоп)

В связи с этим вспомнил байку, подслушанную на лекции.
Встречаются во время перерыва Позняк и Ландау. Л.Д. интересуется, что сейчас проходят студенты.
Позняк отвечает, что теорему о прохождении непрерывной функции через произвольное значение.
Ландау и объявляет, что здесь и доказывать нечего, и рисует график. На что И.Г.
и говорит, мол, позвольте, вы же в ваших книгах все строго обосновываете.
Пришлось Ландау согласиться, что и от своих студентов того же требует )

[Anton_Peplov]

Del.

[sydorov]

Уважаемый Anton_Peplov,

в очередной раз Вас благодарю.

Разобрался с понятием произвольного линейного оператора, хотя было не легко. Наверное, из-за термина произвольный и одновременного требования биективности и понижения ранга.

Anton_Peplov в сообщении #1710455 писал(а):

Упражнение. Постройте изоморфизм двух произвольных $n$-мерных линейных пространств.

Пусть $V$ и $W$ - два линейных пространства, такие, что $\dim V = \dim W = n$
И пусть $e_1,...,e_n$ - базис в $V$ и $g_1,...,g_n$ - базис в $W$

Пусть ЛО $A: V \to W$ действует по правилу $A(e_i) = g_i (i = 1,...,n)$

Для произвольного $\vec v \in V$
$\vec v = \sum_{i=1}^{n} a^{i}\vec e_{i}$
верно, что
$A(\vec v) = \sum_{i=1}^{n} a^{i}\vec g_{i}$

Линейность очевидна

Воспользуемся доказанным выше утверждением, что любой линейный оператор $V \to V$ (аналогично для $V \to W$), для которого прообраз $\vec 0$ - $\vec 0$ - изоморфизм.

Если $A(\vec 0) = \vec 0 \in W$, то $\sum_{i=1}^{n} a^{i}\vec g_{i} = \vec 0$. Следовательно, $\forall a^{i} = 0$
Получаем, что $\operatorname{Ker}A = \vec 0$
Следовательно, построенный ЛО $A$ является изоморфизмом.

Anton_Peplov в сообщении #1710455 писал(а):

sydorov
Рассмотрим, например, линейный оператор $A(x \vec i + y \vec j + z \vec k) = x \vec j + 2y \vec k$ (покажите, что он линейный).

Из правой части можем заключить, что $A$ действует на базис следующим образом

$A(\vec i) = \vec j,$
$A(\vec j) = 2 \vec k$,
$A(\vec k) = \vec 0$,

Пусть $\vec v_1 = x_1 \vec i + y_1 \vec j + z_1 \vec k$ и $\vec v_2 = x_2 \vec i + y_2 \vec j + z_2 \vec k$

Тогда

$A(\vec v_1 + \vec v_2) = A((x_1 + x_2) \vec i + (y_1 + y_2) \vec j + (z_1 + z_2) \vec k) =$
$=(x_1 + x_2) A(\vec i) + (y_1 + y_2) A(\vec j) + (z_1 + z_2) A(\vec k) =$
$= (x_1 + x_2) \vec j + (y_1 + y_2) 2 \vec k = x_1 \vec j + 2 y_1 \vec k + x_2 \vec j + 2 y_2 \vec k = A(\vec v_1) + A(\vec v_2)$

Первое свойство линейности показано.

Пусть $\vec v = x \vec i + y \vec j + z \vec k$ и $\forall \lambda \in \mathbb R$

$A(\lambda \vec v) = A((\lambda x) \vec i + (\lambda y) \vec j + (\lambda z) \vec k) = (\lambda x) A(\vec i) + (\lambda y) A(\vec j) + (\lambda z) A(\vec k) =$
$= (\lambda x) \vec j + 2 (\lambda y) \vec k = \lambda (x \vec j + 2 y \vec k) = \lambda A(\vec v)$

Показано второе свойство.

[sydorov]

Уважаемый Anton_Peplov, я ведь правильно понимаю, что $A(x \vec i + y \vec j + z \vec k) = x \vec j + 2y \vec k$ пример произвольного оператора? Так как $r(A) = 2 < 3$ и он изоморфизм.

[Anton_Peplov]

Del.

[sydorov]

Уважаемый Anton_Peplov,

Anton_Peplov в сообщении #1710626 писал(а):

Но его можно собрать из двух простых частей, представить как композицию двух линейных операторов.

"И тогда этот оператор $A$ (композиция) будет изоморфизмом". Если я правильно продолжаю Вашу фразу, то, благодарю Вас за усилия, стало понятнее )

Anton_Peplov в сообщении #1710626 писал(а):

Обычно ни в учебниках, ни на лекциях так не делают. Я просто пытаюсь откликнуться на Ваш запрос "понять, как устроены линейные операторы".

Дорогой Anton_Peplov! Благодаря Вашим именно неформальным объяснениям, мне кажется, я уже избавляюсь от тотального непонимания "Что же я изучаю".
Можно сказать, что начинаю "мыслить векторно-пространственными образами" и ключевым объектом в них являются линейные операторы. Понимаю, глупо звучит.
Для меня огромная удача, что Вы начали именно с этой темы.

Это не значит, что у меня не осталось вопросов ) Их слишком много. Более всего хотелось бы поговорить о формах (билинейных, квадратичных) и их преобразованиях.
Есть и технические вопросы. Например, откровенно "вымораживает" высказывание "линейная оболочка, натянутая на векторы".

[Anton_Peplov]

sydorov
Мне тут любезно подсказали в личных сообщениях, что я допустил оплошность в своих объяснениях про произвольный линейный оператор и невольно ввел Вас в заблуждение, за что прошу меня простить. Про изоморфизмы я все объяснял верно, а с произвольными операторами переупростил ситуацию: хотел быть понятнее, а в результате допустил фактическую ошибку. Давайте пока оставим эту тему. Я не преподаватель, может быть, они сумеют объяснить лучше.

sydorov в сообщении #1710641 писал(а):

Есть и технические вопросы. Например, откровенно "вымораживает" высказывание "линейная оболочка, натянутая на векторы".

Ну это, по-моему, "масло масляное". Либо линейная оболочка системы векторов, либо, что то же самое, подпространство, натянутое на систему векторов. Если ни то ни другое не нравится, можно говорить "минимальное подпространство, содержащие эти векторы" - это верно по смыслу.

Тут все просто. Возьмем линейное пространство $V$. Пересечение любых его подпространств есть его подпространство (докажите). Пусть есть система векторов $\vec a, \vec b, \vec c, \dots...$. Пересечение всех подпространств, содержащих эти векторы, и есть линейная оболочка этой системы векторов. Она же - минимальное пространство, их содержащее.

[sydorov]

Уважаемый Anton_Peplov,

Anton_Peplov в сообщении #1710646 писал(а):

Пересечение любых его подпространств есть его подпространство (докажите).

Пусть $W$ - пересечение некоторых подпространсв $W_1,...,W_k \subseteq V.$

$\forall W_i \subseteq V (i = 1,...,k):$
1) $\vec 0 \in W_i.$
2) Пусть $\forall \vec v_1, \vec v_2 \in W.$ $W$ - пересечение, значит $\vec v_1 \in W_i$ и $\vec v_2 \in W_i$. Так как $W_i $- подпространство, то $\vec v_1 + \vec v_2 \in W_i.$ Следовательно, $\vec v_1 + \vec v_2 \in W.$
3) $\forall \lambda \in \mathbb R$ и $\forall \vec v \in W.$ Тогда $\vec v \in W_i$, а так как $W_i$ - подпространство, то $\lambda \vec v \in W_i.$ Следовательно, $\lambda \vec v \in W.$

Anton_Peplov в сообщении #1710646 писал(а):

любезно подсказали

Понимаю Ваше желание объяснить это понятие максимально доступно. Вижу даже положительную сторону - лучше заострю на нем внимание в дальнейшем, особенно, если кто-то из участников форума любезно пожелает объяснить )

[Anton_Peplov]

sydorov
Ваше доказательство верно. Однако Вы зря ограничились случаем конечного числа подпространств ($k$). Доказательство сохраняет силу, даже если у пространства бесконечно много подпространств. А уже у плоскости их бесконечно много (докажите). И, следовательно, у любого двумерного пространства над $\mathbb R$ - тоже (почему?).

Правда, подпространства одной размерности изоморфны друг другу. Так что подпространства $n$-мерного пространства ($n>1$) распадаются на $n$ классов по размерности: ровно одно нульмерное (почему одно?), ровно одно $n$-мерное (почему одно?) и еще $n-1$ классов подпространств, от одномерных до $n-1$-мерных.

Сложнее дело обстоит в пространствах бесконечной размерности: там бесконечно много неизоморфных друг другу подпространств. Но в бесконечномерных пространствах вообще многое сложнее, и их обычно изучают не в линейной алгебре, а в функциональном анализе.