Некоторые вопросы по интегральному исчислению

[skobar]

Solaris86 в сообщении #1709438 писал(а):

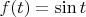
Тут, на мой взгляд, неоднозначный момент: если построить графики $f(x) = \sin x$, $f(t) =\sin t$ и $f(z) = \sin z$, то эти графики полностью наложатся друг на друга, то есть при одинаковых численных значениях этих разных переменных значения функции будут равны.
То есть можно сказать, что:
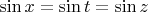
1. $\sin x=\sin t=\sin z$, если $x = y = t$, то есть при разных значениях разных переменных;
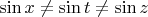
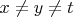
2. $\sin x \not=\sin t \not =\sin z$, если $x \not = y \not = t$, то есть при одинаковых значениях разных переменных.

Боюсь, что вас запутали. Попытаюсь распутать :)
Неопределенный интеграл - это семейство функций (отличающихся на константу), то есть это множество, элементами которого являются функции. И какое бы обозначение для переменной интегрирования в неопределенном интеграле мы не использовали, результатом будет одно и то же множество, состоящее из одних и тех же функций. Что такое функция? Это тройка объектов - область определения, область значений, и правило, по которому каждому элементу из области определения сопоставляется какой-то (один) элемент из области значений. Две функции считаются равными, если соответствующие объекты для них совпадают. Обращаю внимание, что в определении функции неважно, какую букву мы будем использовать для обозначения переменной, это все равно будет одна и та же функция.
У вас абсолютно правильная мысль про графики - если у двух функций графики совпадают, то это одна и та же функция, и неважно, какое обозначение переменой используется.
Отмечу ещё, что нужно различать функцию и значение функции в точке - это разные вещи. Если речь идет о равенстве функций, то неважно, какой буквой обозначается переменная. Но если мы говорим о равенстве значений функций в точке, то, понятно, $f(x)$ и $f(y)$ - это не одно то же.

[Solaris86]

skobar
Ваш пост мне более понятен, так как то, о чём вы пишете, перекликается с моим представлениями.
Тогда может вы прокомментируете по поводу независимости обозначения переменной для неопределённого и определённого интегралов? Потому пока я так и не понял, в чём смысл выделения этого факта в отдельное свойство интегралов...
У нас не в других разделах математики нет отдельных свойств про обозначение переменных. Я, например, не видел, чтобы где-то отдельно прописывалось, что при построении графиков функции можно выбирать любое обозначение переменной и график функции от этого не поменяется. Это не прописывается, потому что это и так очевидно...
Выше Someone писал про замену переменной в интеграле, но я всё равно не пойму, при чём тут независимость обозначения переменной, вроде так же очевидно, что при замене переменной в интеграле можно использовать любое обозначение переменной...

[skobar]

Solaris86 в сообщении #1709469 писал(а):

вроде так же очевидно, что при замене переменной в интеграле можно использовать любое обозначение переменной...

Совершенно верно, это очевидно, причем как для определённого, так и для неопределенного интегралов. Результат не будет зависеть от обозначения переменной интегрирования в обоих случаях. На мой взгляд, это настолько очевидно, что нет нужды выписывать это как отдельное свойство, но, может быть, это имеет какой-то (неизвестный мне) смысл с точки зрения обучения.

[Someone]

(skobar)

skobar в сообщении #1709387 писал(а):

Как семейство функций неопределенный интеграл не зависит от обозначения переменной интегрирования.

Вы точно знаете, что поле действительных чисел существует в единственном экземпляре?
Конечно, пользуясь тем, что между двумя экземплярами поля действительных чисел существует только один изоморфизм, мы можем однозначно установить изоморфизм двух множеств первообразных. Но, например, для поля комплексных чисел это не так.

[skobar]

(Someone)

Someone в сообщении #1709546 писал(а):

Вы точно знаете, что поле действительных чисел существует в единственном экземпляре?
Конечно, пользуясь тем, что между двумя экземплярами поля действительных чисел существует только один изоморфизм, мы можем однозначно установить изоморфизм двух множеств первообразных. Но, например, для поля комплексных чисел это не так.

Речь не о том, что между двумя множествами первообразных можно установить изоморфизм. Независимо от того, какое обозначение для переменной интегрирования используется, в результате получится в точности одно и то же множество функций. Нет никакой нужды устанавливать изоморфизм одного и того же множества на себя.

[Someone]

(skobar)

skobar в сообщении #1709557 писал(а):

Речь не о том, что между двумя множествами первообразных можно установить изоморфизм. Независимо от того, какое обозначение для переменной интегрирования используется, в результате получится в точности одно и то же множество функций. Нет никакой нужды устанавливать изоморфизм одного и того же множества на себя.

На самом деле там возникают определённые проблемы на уровне теории множеств. Но ладно, не будем развивать тему. Кстати, подумайте всё-таки, почему утверждение об инвариантности формул интегрирования формулируют как "если $\int f(x)dx=F(x)+C$, то $\int f(u)du=F(u)+C$", а не как "$\int f(x)dx=\int f(u)du$". Хотя, по вашему утверждению, "как множества они совпадают, и написать знак равенства — не грех". И даже $f(x)=f(u)$ не пишут, хотя, по вашему утверждению, это одна и та же функция.

[skobar]

(Someone)

Someone в сообщении #1709572 писал(а):

На самом деле там возникают определённые проблемы на уровне теории множеств. Но ладно, не будем развивать тему.

Не вижу никаких проблем

Someone в сообщении #1709572 писал(а):

Кстати, подумайте всё-таки, почему утверждение об инвариантности формул интегрирования формулируют как "если $\int f(x)dx=F(x)+C$, то $\int f(u)du=F(u)+C$", а не как "$\int f(x)dx=\int f(u)du$"

Чего только не пишут, но это не отменяет совершенно однозначное определение неопределенного интеграла (невзначай получился каламбур :) )

Someone в сообщении #1709572 писал(а):

И даже $f(x)=f(u)$ не пишут, хотя, по вашему утверждению, это одна и та же функция.

Я такого не писал. Когда имеют ввиду именно функцию, то обычно пишут просто $f$. Иногда, допуская некоторую вольность функцию записывают как $f(x)$, что технически не совсем корректно, т.к. так же обозначается значение функции в точке $x$.

[wrest]

Solaris86 в сообщении #1709363 писал(а):

Встречал. Меня всегда это ставило в тупик.

Это простое следствие ограниченности набора "элементарных функций". Тех, что мы называем "элементарные функции" просто не хватает на все интегралы. Поэтому есть всякие интегральные логарифмы и подобные, которые нельзя записать элементарными функциями и для них придумали свои обозначения.

В математике кстати синус и косинус это не только отношение катета к гипотенузе. Определения разные и одно из них примерно такое: синус и косинус это периодичесаие функции такие, что вторая производная равна самой функции с обратным знаком. То есть такую периодическую функцию, что является решением такого-то дифура с начальным условием таким-то, отныне нарекаем синусом.

[Solaris86]

Всем спасибо за помощь по предыдущим вопросам!
Следующие непонятные моменты уже из технических приложений интеграла.
Интересуют интеграл свёртки и автокорреляционная функция.
Интеграл свёртки

Автокорреляционная функция

Здесь у меня непонимание, почему где-то функция от $t$, где-т от $\tau$ и, соответственно, переменная интегрирования где-то $dt$, где-то $d\tau$, хотя в обоих случаях ось времени обозначается $t$, а $\tau$ - это некоторый момент времени на этой оси.

[Евгений Машеров]

(Оффтоп)

А почему иногда пишут Ирак, а иногда Иран?

Нас интересует зависимость сигнала в данный момент времени от сигналов в другие моменты времени. Для этого мы считаем корреляцию сигнала с ним же, но сдвинутым по времени. Сдвиг по времени обозначен "тау". Мы полагаем, что зависимость эта сохраняется всё время и неизменна, поэтому интеграл берётся по всему времени его существования t. То есть для автокорреляционной функции тау это сдвиг, для которого мы желаем знать корреляцию с несдвинутым сигналом.
Для свёртки - тау это обычное время, в которое испускается сигнал $f(\tau)$, который порождает отклик $h(t)$, длящийся некоторое время (Вовочка кидает камешки в колокол, попадания камешков описываются $f(\tau)$,, звук от отдельного попадания получается $h(t)$, а звук, слышимый в настоящий момент, получается суммированием звуков, порождённых в прошлом, для чего мы умножаем входной сигнал f на отклик h с учётом, насколько отставлен сигнал в определённый момент времени от настоящего времени, и всё суммируем (интегрируем)

[Someone]

(skobar)

skobar в сообщении #1709579 писал(а):

Someone в сообщении #1709572 писал(а):

Кстати, подумайте всё-таки, почему утверждение об инвариантности формул интегрирования формулируют как "если $\int f(x)dx=F(x)+C$, то $\int f(u)du=F(u)+C$", а не как "$\int f(x)dx=\int f(u)du$"

Чего только не пишут, но это не отменяет совершенно однозначное определение неопределенного интеграла (невзначай получился каламбур :) )

А я разве предъявлял какие-нибудь претензии к определению неопределённого интеграла?
Ну хорошо. Мы знаем, что $\int\cos x\,dx=\sin x+C$. Стало быть, $\int\cos\sin x\,d\sin x=\sin\sin x+C$.
Равны ли эти множества функций?

[skobar]

(Someone)

Someone в сообщении #1709768 писал(а):

Мы знаем, что $\int\cos x\,dx=\sin x+C$. Стало быть, $\int\cos\sin x\,d\sin x=\sin\sin x+C$.

Насколько я понимаю, в исходном равенстве $x$ заменяется на $\sin x$. Так действовать нельзя, потому что равенство $\int\cos x\,dx=\sin x+C$ - это не поточечное равенство двух функций. Его следует понимать в том смысле, что любая функция из левой части может быть записана в виде $\sin x+C$. Строго говоря, такая запись не совсем корректна, но так уж сложилось.
Если быть абсолютно строгим, то правую часть равенства следует записывать так:
$\{f:\mathbb{R}\rightarrow\mathbb{R}\,|\, \exists C\in\mathbb{R}\, s.t.\, \forall x\in \mathbb{R}\, f(x)=\sin x + C \}$

[Someone]

(skobar)

skobar в сообщении #1709772 писал(а):

Насколько я понимаю, в исходном равенстве $x$ заменяется на $\sin x$. Так действовать нельзя

То есть, Вы запрещаете делать замену переменной в неопределённом интеграле.

[skobar]

(Someone)

Someone в сообщении #1709783 писал(а):

То есть, Вы запрещаете делать замену переменной в неопределённом интеграле.

С чего вы это взяли? Ничего подобного я не писал. Цитируйте все утверждение корректно целиком - оно не про левую часть равенства, а про все равенство. В вашей импликации выше вы действовали как будто равенство представляет собой поточечное равенство двух функций, что не так. Прочитайте написанное внимательно.