Абракадабра какая-то. Уравнение касательной к линии

в точке

имеет вид
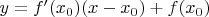
. Можно, конечно, обозначить

.
Да, ошибся со знаки и обозначениями.
Да??? Если Вы имеете в виду
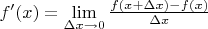
, то это не аналитическое выражение. Во всяком случае, оно не более "аналитическое", чем выражение для первообразной.
Именно это и имею в виду. Просто подобного выражения для первообразной вообще нигде не видел, во всех учебниках как под копирку просто даётся "на веру" обозначение неопределённого и всё. Тот, кто ввёл это обозначение неопределённого в 17 веке явно не с потолка это придумал, а с какой-то целью именно так решил обозначать неопределённый интеграл. При этом с определённым интегралом всё более или менее понятно, во всех книгах приводят доказательство теоремы с формулой Ньютона-Лейбница. Если неопределённый интеграл - это просто символическая запись, которая по сути своей ничего не значит (я про знак интегрирования, производную и дифференциал аргумента), тогда так бы и писали, чтобы не было лишних вопросов.
Единственное, что мне приходит на ум по поводу такого обозначения неопределённого интеграла, так то, что оно такое, чтобы могли выполняться известные свойства:
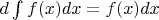
и
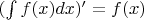
Так что, думаю, этот вопрос про обозначение неопределённого интеграла можно закрыть.
Также можно закрыть вопрос про аналитическое выражение для первообразной, поскольку, видимо, его вообще не существует и существовать не может, просто никто из форумчан не захотел писать в такой формулировке.
-- 15.11.2025, 19:10 --Вы не встречали такое выражение — "неберущийся интеграл"? Типа, например,
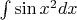
или
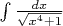
.
Встречал. Меня всегда это ставило в тупик.
-- 15.11.2025, 19:34 --Тогда следующий вопрос - это одно непонятное свойство интеграла.
Звучит оно так:
Интеграл не зависит от символа, используемого для обозначения переменной интегрирования.
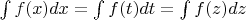 https://portal.tpu.ru/SHARED/k/KONVAL/S ... /12/05.htm
https://portal.tpu.ru/SHARED/k/KONVAL/S ... /12/05.htmФормулировка о независимости интеграла от используемого для переменной интегрирования символа ставит в тупик, я вообще не понимаю, для чего этот факт выделен в отдельное свойство. Я вообще волен выбирать любые символы для переменных, математикf вроде не накладывает ограничений на обозначения переменных...
Ладно бы ещё речь шла о том, что

- это незавиcимая переменная,

- зависимая от

переменная
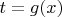
,

- зависимая от y переменная
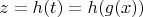
, тогда бы я понял, что речь идёт об инвариантности формулы интегрирования... Но в данной формулировки нет никаких уточнений про переменные, независимые они или зависимые, поэтому и не понятно, что хотят сказать эти свойством.