но есть вещи которые при уменьшении не только становятся нулевыми
Так
докажите что количество исключений именно таково! Математически докажите, а не проверкой ничтожной части всех чётных натуральных чисел. Потому что есть примеры когда количество уменьшается, даже до нуля, но не исчезает, т.е. всегда продолжают появляться и количества больше нуля. А Вы даже этих примеров не понимаете и считаете что они к теме не относятся. Ещё как относятся.
Ещё проще пример: зададимся длиной интервала

, будем проверять сколько простых чисел в таком интервале начиная с

(т.е. числа в интервале
![$[N,N+L-1]$ $[N,N+L-1]$](https://dxdy-01.korotkov.co.uk/f/0/a/0/0a0a1a3b5a6ba7ce45c54c813664d1d782.png)
). С ростом

количество простых чисел в любом таком интервале уменьшается (и тоже не монотонно). Начиная с некоторого большого числа
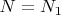
будут встречаться интервалы длиной

в которых вообще нет простых чисел. Т.е. количество простых чисел в них равно нулю. Однако для любого значения

всегда найдётся такое
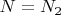
, что в нём будет простое число. Т.е. уменьшение, даже до нуля, не означает исчезновения.
Значит уменьшением нельзя аргументировать исчезновение. Что в этом непонятного?
Уж сколько раз повторять, если бы я смог самостоятельно доказать, то я бы не стал здесь, на форуме математиков, писать про это. Зачем мне это было бы нужно. А?
Я написал, что:
1. Каждое четное число порождает множество пар чисел дающих в сумме это четное число.
2. Каждое такое множество состоит из четырех подмножеств (С-С, С-П, П-С, П-П : где С - составное, П - простое). Четные числа исключаем, т.к они не интересны для нас.
3. Происходит глобальное увеличение количества пар П-П, при некоторых локальных уменьшениях, при росте четного числа N.
Что не так?