Впервые этот критерий доказал сотрудник Института прикладной математики имени М.В. Келдыша Садов С.Ю., судя
по препринту, в 2003 году.
По-моему, достаточные условия выпуклости четырехугольника, приводимые в этой работе, неверны.
Условия:
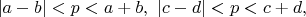
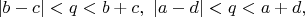
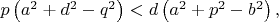
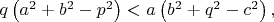
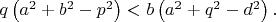
Контрпример:
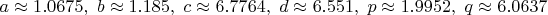
Код:
f1(a,b,c,d,e,f) := a^2*c^2*(b^2+d^2+e^2+f^2-a^2-c^2) + b^2*d^2*(a^2+c^2+e^2+f^2-b^2-d^2)+
e^2*f^2*(a^2+c^2+b^2+d^2-e^2-f^2) - a^2*b^2*e^2-b^2*c^2*f^2-c^2*d^2*e^2-d^2*a^2*f^2 ;
f2(a,b,c,d,e,f) := e*(a*b+c*d) - f*(a*d+b*c) ;
a0 : 1.06750887 ; b0 : 1.18500603 ; c0 : 6.77639952 ; d0 : 6.55124523 ;
e0 : 1.99520172 ; f0 : 6.06370749 ;
float(f1(a0,b0,c0,d0,e0,f0));
float(f2(a0,b0,c0,d0,e0,f0));
h1(a,b,c,d,e,f) := e*(a^2+d^2-f^2) - d*(a^2+e^2-b^2) ;
h2(a,b,c,d,e,f) := f*(a^2+b^2-e^2) - a*(b^2+f^2-c^2) ;
h3(a,b,c,d,e,f) := f*(a^2+b^2-e^2) - b*(a^2+f^2-d^2) ;
float(h1(a0,b0,c0,d0,e0,f0));
float(h2(a0,b0,c0,d0,e0,f0));
float(h3(a0,b0,c0,d0,e0,f0));